Mathematics
8 DESCARTES.
Theory of Equations
It is necessary that I make some general statements concerning the nature of equations, that is, of sums composed of several terms, in part known, in part unknown, of which some are equal to the others, or rather, all of which considered together are equal to zero, because this is often the best way to consider them.
Know then that in every equation there are as many distinct roots, that is, values of the unknown quantity, as is the number of dimensions of the unknown quantity.2
Suppose, for example,

or
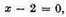 3
3 and again,
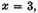
or
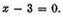
Multiplying together the two equations
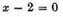
and
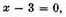
we have
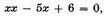
or
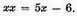
This is an equation in which
x has the value 2 and at the same time
x has the value 3. If we next make
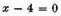
and multiply this by
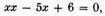
we have
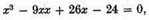
another equation, in which
x, having three dimensions, has also three values, namely, 2, 3, and 4.
It often happens, however, that some of the roots are false, or less than nothing. Thus, if we suppose x to represent the defect4 of a quantity 5, we have
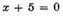
which, multiplied by
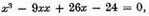
gives
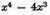
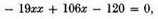
as an equation having four roots, namely three true roots, 2, 3, and 4, and one false root, 5.
It is evident from this that the sum of an equation containing several roots is always divisible by a binomial consisting of the unknown quantity diminished by the value of one of the true roots, or plus the value of one of the false roots. In this way, the dimension of an equation can be lowered.
On the other hand, if the sum of an equation is not divisible by a binomial consisting of the unknown quantity plus or minus some other quantity, then this latter quantity is not a root of the equation. Thus the last equation
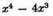
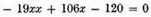
is divisible by
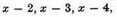
and
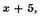
but is not divisible by
x plus or minus any other quantity, which shows that the equation can have only the four roots, 2, 3, 4, and 5.
We can determine from this also the number of true and false roots that any equation can have, as follows: An equation can have as many true roots as it contains changes of sign, from + to - or from - to +; and as many false roots as the number of times two + signs or two - signs are found in succession.5 Thus, in the last equation, since +x4 is followed by -4x3, giving a change of sign from + to -, and - 19xx is followed by + 106x and + 106x by - 120, giving two more changes, we know there are three true roots; and since -4x3 is followed by - 19xx there is one false root.
It is also easy to transform an equation so that all the roots that were false shall become true roots, and all those that were true shall become false. This is done by changing the sign of the second, fourth, sixth, and all even terms, leaving unchanged the signs of the first, third, fifth, and other odd terms. Thus, if instead of
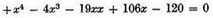
we write
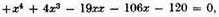
we get an equation having only one true root, 5, and three false roots, 2, 3, and 4.
If the roots of an equation are unknown and it be desired to increase or diminish each of these roots by some known number, we must substitute for the unknown quantity another quantity greater or less by the given number.6 Thus, if it be desired to increase by 3 the value of each root of the equation
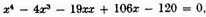
put y in the place of x, and let y exceed x by 3, so that
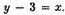
Then for
xx put the square of

or
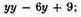
for
x3 put its cube,
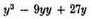
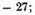
and for
x4 put its fourth power [
quarré de quarré], or
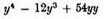
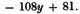
Substituting these values in the above equation, and combining, we have
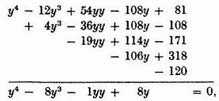
or

whose true root is now 8 instead of 5, since it has been increased by 3.
If, on the other hand, it is desired to diminish by 3 the roots of the same equation, we must make
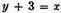
and
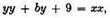
and so on, so that instead of
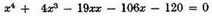
we have
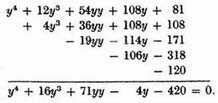
It should be observed that increasing the true roots of an equation diminishes the false roots by the same amount; and on the contrary diminishing the true roots increases the false roots; while diminishing either a true or a false root by a quantity equal to it makes the root zero; and diminishing it by a quantity greater than the root renders a true root false or a false root true. Thus by increasing the true root 5 by 3, we diminish each of the false roots, so that the root previously 4 is now only 1, the root previously 3 is zero, and the root previously 2 is now a true root, equal to 1, since
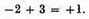
This explains why the equation
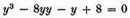
has only three roots, two of them, 1 and 8, being true roots, and the third, also 1, being false; while the other equation
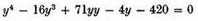
has only one true root, 2, since
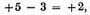
and three false roots, 5, 6, and 7.
1 As we have said, Descartes’s relation to Viète is not clear. The same holds for his relation to the English mathematician and astronomer Thomas Harriot (1560–1621), also known for his description of newly named Virginia (1588). Harriot wrote (probably about 1610) the influential Artis analyticae praxis (London, 1631), with a theory of equations which in several aspects anticipates Descartes’s treatment. He wrote
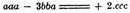
for our
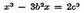
(see Selection I.2) and used > and in our present sense:
Signum majoritatis ut
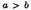 significat a majorem quam b.
significat a majorem quam b. John Wallis (1616–1703), in his
Treatise of algebra (Oxford, 1685), claimed that Descartes borrowed heavily from Harriot: "Hariot hath laid the foundations on which Des Cartes (though without naming him) hath built the greatest part (if not the whole) of his Algebra or Geometry." Wallis missed the point, but his statement foreshadows the tension between English and Continental mathematicians typified in the later Newton-Leibniz priority struggle. See J. F. Scott,
The mathematical work of John Wallis (Taylor and Francis, London, 1938), chap. IX.
2 This is Descartes’s formulation of the fundamental theorem of algebra. For its further, more exact, formulation and proof, see Selections II.6 on Girard, II.10 on Euler, and II.12 on Gauss.
3 Descartes writes: "x equal to 2 or

equal to nothing, and again
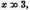
or
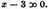
He does not use the sign =, already introduced by Recorde and Harriot; see note 1.
4 A defect [défaut] is the negative of a positive number; thus -5 is the defect of 5, that is, the remainder when 5 is subtracted from zero.
5 This is the sign rule as stated by Descartes. It was formulated in a more precise manner by Isaac Newton in his Arithmetica universalis (Cambridge, 1707) and by C. F. Gauss in "Beweis eines algebraischen Lehrsatzes," Crelle’s Journal [figure table]
die reine und angewandte Mathematik 3 (1828), 1–4; Werke, III, 65–70. We now can express it in the following way: If
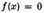 is an equation of degree n with real coefficients, where
is an equation of degree n with real coefficients, where
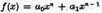
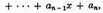 then the number of positive roots is equal to or an even number less than the number of variations in the signs of successive terms. Multiple roots have to be counted in accordance with their multiplicity, and zero is not a positive root.
then the number of positive roots is equal to or an even number less than the number of variations in the signs of successive terms. Multiple roots have to be counted in accordance with their multiplicity, and zero is not a positive root.
6 This change of variable of an equation by means of substitution of the type
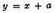
is not new, and is, as we observed in Selection II.4, note 8, one of the substitutions used by Cardan in his
Ars magna (1545). Descartes here shows its use in the search for positive and negative roots. The notation, as elsewhere in Descartes’s writings, strikes us as quite modern.