The Wave Theory of Light

Huyghens

Proofs in optics, as in every science in which mathematics is applied to matter, are founded upon facts from experience—as for example, that light moves in straight lines, that the angles of incidence and reflection are equal, and that light rays are refracted in accordance with the law of sines [i.e., that the ratio between the sines of the incident and refracted ray is constant for the same substance.] For this last law is now as generally and surely known as either of the others.

Most writers in optics have been content to assume these facts, but others more curious have attempted to discover the source and reason of these phenomena, looking upon them as being in themselves interesting data. Yet although they have propounded some ingenious theories, intelligent readers still require a fuller explanation before being entirely satisfied. Therefore I herein offer some considerations on the matter with the hope of making clearer this branch of physics which has not improperly gained the reputation of being very obscure.

I feel myself particularly indebted to those that first began to study these profound subjects, and to lead us to hope them capable of orderly explanation . . . Yet I have been surprised to find these very investigators accepting arguments far from clear as if proof conclusive. No one has yet offered even a probable explanation of the first two remarkable phenomena of light,—why it moves in straight lines, and why rays from any and all directions can cross one another without interference.

I shall attempt in this treatise to submit clearer and more probable reasons, along the lines of modern philosophy, first for the transmission of light, and, second, for its reflection when it meets certain bodies.

Further, I shall explain the fact of rays said to undergo refraction in passing through various transparent bodies. Here I shall consider also, the refractions due to the differing densities of the atmosphere. Later I shall investigate the remarkable refraction occurring in Icelandic crystals. Finally, I shall study the different shapes necessary in transparent and reflecting bodies in order to bring together rays upon a single point or to deflect them in different ways. Here we shall see how easy it is by our new theory to determine not alone the ellipses, hyperbolas, and other curves which M. Descartes has so shrewdly constructed for this end, but as well the curve that one surface of a lens must have when the other surface is known, as spherical, plane, or any other figure.

We cannot but believe that light is the motion of a certain material. Thus when we reflect on its production, we discover that here on the earth it is usually emitted from fire and flame, and that these unquestionably contain bodies in rapid motion, since they can soften and melt many other more solid substances. If we note its effects, we see that when light is brought to a point, as, for example, by concave mirrors, it can cause combustion the same as fire: that is, it can force bodies apart, a power that certainly argues motion, at least in that true science where one believes all natural phenomena to result from mechanical causes. Moreover, in my mind we must either admit this or give up all hope of ever understanding anything in natural science.

Since, according to this philosophy, it is believed certain that the sensation of sight is produced only by the impulse of some form of matter against the nerves at the base of the eye, we have yet another reason for believing light to be a motion in the substance lying between us and the body producing the light.

As soon as we consider, moreover, the enormous speed with which light travels in every direction, and the fact that when rays come from different directions, even from those exactly opposite, they cross without interference, it must be plain that we do not see luminous objects by means of particles transmitted from the objects to us, as a shot or an arrow moves through the air. For surely this would not allow for the two qualities of light just mentioned, particularly the latter (that of speed). Light, then, is transmitted in some other way, a comprehension of which we may get from our knowledge of how sound moves through the air.

We know that sound is sent out in all directions through the medium of the air, a substance invisible and impalpable, by means of a motion that is communicated successively from one part of the air to the next; and as this movement has the same speed in all directions, it must form spherical surfaces that keep enlarging until at last they strike the ear. Now there can be no doubt that light likewise reaches us from a luminous substance through some motion caused in the matter lying in the intervening space,—for we have seen above that this cannot take place through the transmission of matter from one place to another.

If, moreover, light requires time for its passage—a matter we shall discuss in a moment—it will then follow that this movement is caused in the substance gradually, and therefore is transmitted, like sound, by surfaces and spherical waves. I call these waves because of their likeness to those formed when one throws a pebble into water, which are examples of gradual propagation in circles, although from a different cause and on a plane surface.

In regard to the question of light requiring time for its transmission, let us consider whether there is any experimental evidence against it.

What experiments we can make here on the earth with sources of light placed at great distances (although indicating that it does not take a sensible time for light to pass over these distances) are subject to the objection that these distances are yet too small, and that we can only argue that the movement of light is enormously fast. M. Descartes thought it to be instantaneous and based his opinion upon much better reasons taken from the eclipse of the moon. Yet as I shall make clear, even this evidence is not decisive. I shall state the matter in a somewhat different way from his in order to more easily exhibit all the consequences.

Suppose S to be the position of the sun, E A part of the orbit of the earth, S E M a straight line intersecting in M, the orbit of the moon, represented by the circle A M.

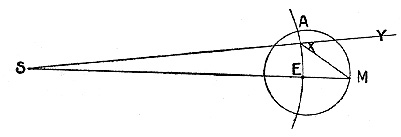
Now if light requires time—say an hour—to move the distance between the earth and the moon, then [at the time of an eclipse] it follows that when the earth has come to E its shadow, or the stoppage of the light of the sun, will not yet have reached M [the moon], and will not for an hour. Counting from the instant the earth reaches E, it will be an hour before will reach M if it is to be obscured there. This eclipse will not be seen from the earth for yet another hour. Suppose that during these two hours the earth has moved to X, the moon appearing eclipsed at M, the sun still being seen at S. For I assume as does Copernicus that the sun is fixed and since light moves in straight lines, is always seen in its true position.

But as a matter of fact, we are assured that the eclipsed moon always appears directly opposite the sun; while on the above supposition [that light takes an hour in passing between the moon and the earth], its position ought to be back of the straight line by the angle Y X M, the supplement of the angle S X M. But this is not the case, for this angle Y X M would be very easily noticed, it being about 33 degrees. For by our analysis (found in the essay on the causes of the phenomena of Saturn), the distance from the sun to the earth, S E, is about 12,000 times the diameter of the earth, and hence 400 times the distance of the moon, which is 3° diameters. The angle X M E then will be nearly 400 times as great as E S X, which is 5 minutes, i.e., the angular distance travelled by the earth in two hours [the earth traversing almost a degree in a day]. Thus the angle E M X is almost 33 degrees, and likewise the angle M X Y, being 5 minutes greater [than E M X].

Now it must be remembered that in this computation it is assumed that the speed of light is such as to consume an hour in passing from here to the moon. But if we assume it to take only a minute of time, then the angle Y X M would amount to only 33 minutes, and if it only takes ten seconds, this angle will be less than six minutes. Now so small an angle is not observable in a lunar eclipse and hence it is not permissible to argue that light is absolutely instantaneous.

It is rather unusual, we admit, to take for granted a speed 100,000 times as great as that of sound, which (following my experiments) travels about 180 toises [about 1150 feet] in a second, or during a pulse-beat. Yet this supposition is not at all impossible, for it is not necessary to carry a body at such speed but only for motion to traverse successively from one point to another.

Hence I do not hesitate in this matter to assume that the passage of light takes time, for on this assumption all phenomena can be explained, while on the contrary supposition none of them can be explained. In fact, it seems to me and to many others as well, that M. Descartes, whose purpose has been to discuss all physical matters clearly, and who has certainly succeeded in this better than any one before him, has written nothing on light and its qualities that is not either hard to understand or even incomprehensible.

Moreover, this idea that I have propounded as an hypothesis has lately been made a well nigh established fact by that keen calculation of Roemer, whose method I will here take occasion to describe, on the expectation that he will himself in the future fully confirm this theory.

His method, the same as the one we have just discussed, is astronomical. He shows not only that light takes time for its passage, but calculates also its speed and that this must be at least six times as much as the rate I have just given as an estimate.

In his demonstration he uses the eclipses of the small satellites that revolve around Jupiter, and very frequently pass into his shadow. Roemer’s reasoning is this:

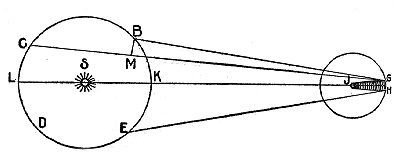
Let S be the sun, B C D E the yearly orbit of the earth, J Jupiter and G H the orbit of his nearest satellite, for this one because of its short period is better suited to this investigation than any one of the other three. Suppose G to be the point where the satellite enters, and H where it leaves, Jupiter’s shadow.

Suppose that when the earth is at B, the satellite is seen to emerge [at G], at some time before the last quarter. Were the earth to remain stationary there, 42½ hours would elapse before the next emergence would take place, for this much time is taken by the satellite in making one revolution in its orbit and returning to opposition to the sun. For example, if the earth remained at B during 30 revolutions, then after 30 times 42½ hours, the satellite would again be seen to emerge. If in the meantime the earth has moved to C, farther from Jupiter, it is clear that if light requires time for its passage, the emergence of the satellite will be seen later when the earth is at C than when at B. For we must add to the 30 times 42½ hours, the time occupied by light in passing over the difference between the distances [of the earth from Jupiter] G B and G C, i.e., M C. So in the other quarter, when the earth travels from D to E, approaching Jupiter, the eclipses will occur earlier when the earth is at E than when at D. [p.147]

Now by many observations of these eclipses throughout ten years, it is shown that these inequalities are actually of some moment, amounting to as much as ten minutes or more: whence it is argued that in traversing the whole diameter of the earth’s orbit, K L, double the distance from the earth to the sun, light takes about 22 minutes.

The motion of Jupiter in its orbit while the earth passes from B to C or from D to E has been taken into consideration in Roemer’s calculation, where it is also proved that these inequalities cannot be caused by any irregularity or eccentricity in the movement of the satellite.

Now if we consider the enormous size of this diameter K L [the earth’s orbit] which I have estimated to be about 24,000 times that of the earth, we get some comprehension of the extraordinary speed of light.

Even if K L were only 22,000 diameters of the earth, a speed traversing this distance in 22 minutes would be equal to the rate of a thousand diameters a minute, i.e., 16 2–3 diameters a second (or a pulse-beat) which makes more than 1,000 times 100,000 toises, since one diameter of the earth equals 2,865 leagues, of which there are 25 to the degree, and since in accordance with the very precise calculation made by Mr. Picard in 1669 under orders from the king, each league contains 2,282 toises.

As I stated before sound moves only 180 toises per second. Hence the speed of light is over 600,000 times as great as that of sound, which, however, is very different from being instantaneous,—it is the difference between any finite number and infinity. The theory that light movements are propagated from point to point in time being thus demonstrated, it follows that light moves in spherical waves, as does sound.

But if they are alike in this regard, they are unlike in others, as in the original cause of the motion that transmits them, the medium through which they move, and the manner in which they are transmitted in it.

We know that sound is caused by the rapid vibration of some body (either as a whole or in part), this vibration setting in motion the adjoining air. But light movements must arise at every point of the luminous body, otherwise all the various parts of the body would not be visible. This fact will be clearer from what follows.

In my judgment, this movement of light-giving bodies cannot be more satisfactorily explained than by supposing that those that are fluid, e.g., a flame, and probably the sun and stars, consist of particles that float about in a much rarer medium, that sets them in violent motion, causing them to strike against the still more minute particles of the surrounding ether. In the case of light-giving solids such as red-hot metal or carbon we may suppose this movement to be caused by the rapid motions of the metal or wood, the particles on the surface exciting the ether. Hence the vibration producing light must be much shorter and faster than that causing sound, since we do not find that sound disturbances give rise to light any more than the wave of the hand through the air causes sound.

The next question is in regard to the nature of the medium through which the vibration produced by light-giving bodies moves. I have named it ether, but it plainly differs from the medium through which sound moves. The latter is simply the air we feel and breathe, and when it is removed from any space, the medium which carries light still remains. This is shown by surrounding the sounding body in a glass vessel, and exhausting the air by means of the air-pump that Mr. Boyle has devised, and with which he has performed so many striking experiments. In trying this experiment, however, it is best to set the sounder on cotton or feathers so that it cannot communicate vibrations to the glass receiver or the air-pump, a point hitherto neglected. Then, when all the air has been exhausted, one catches no sound from the metal when it is struck.

Hence we conclude not only that our atmosphere which cannot penetrate glass is the medium through which sound acts, but that the medium carrying light-vibrations is something different: for after the vessel is exhausted of air, light passes through it as easily as before.

The last point is proven even more conclusively by the famous experiment of Torricelli. [Fill a long closed glass tube with mercury, then invert it.] The top of the glass tube not filled by the mercury contains a high vacuum, but transmits light as well as when filled with air. This demonstrates that there is within the tube some form of matter different from air, and which penetrates either glass or mercury, or both, though both are impenetrable to air. And if a like experiment is tried with a little water on top of the mercury, it becomes equally clear that the substance in question traverses either glass or water or both.

In regard to the different methods of transmission of sound and light, in the case of sound it is easy to see what happens when one remembers that air can be compressed and reduced to a much smaller volume than usual, and that it tends with the same force to expand to its original volume. This quality, considered along with its penetrability retained in spite of such condensation seems to show that it consists of small particles that float about in rapid vibration in an ether consisting of still more minute particles. Sound, then, is caused by the struggle of these particles to escape when at any point in the course of a wave they are more crowded together than at some other point.

Now the wonderful speed of light considered with its other qualities, does not permit us to believe it to be transmitted in the same manner. Therefore I shall try to explain the way in which I think it must take place. I must first, however, describe that quality of hard substances through which they transmit motion one to another. If one take a number of balls of the same size of any hard substance, and place them touching one another in one line, he will find that on letting a ball of the same size strike against one end of the line, the motion is transmitted in an instant to the other end of the line. The last ball is driven from the line while the others are apparently undisturbed, the ball that struck the line coming to a dead stop. This is an illustration of a transmission of motion at great speed, varying directly as the hardness of the balls. Yet it is certain that this transmission is not instantaneous, but requires time. For if the movement, or if you wish, the tendency to move, did not pass from one ball to another in succession, they would all be set in motion at the same instant and would all move forward at the same time. Now this is so far from the case that only the last one leaves the row, and it has the speed of the ball that first struck the line.

There are other experiments, also demonstrating that all bodies, even those thought hardest, such as steel, glass and agate, are really elastic, and bend a little, no matter whether they are in rods, balls, or bodies of any other shape,—that is, they give slightly at the point where struck, and at once regain their former shape. Thus I have discovered that in letting a glass or agate ball strike on a large, thick, flat piece of the same substance the surface of which has been roughened by the breath, the place where it strikes is shown by a circular indentation that varies in size directly as the force of the blow. This indicates that the materials give when struck and then fly back,—an event that necessarily takes time.

Now to apply such a motion to the explanation of light, there is nothing in the way of our imagining the particles of ether to have an almost complete hardness, and an elasticity as perfect as we need wish.We need not here discuss the cause of either this hardness of elasticity, as this would lead us too far from the question at issue. I will remark, however, by the way, that these particles of ether, in spite of their minuteness, are also composed of parts and that their elasticity depends on a very rapid motion of a subtle substance traversing them in all directions and making them take a structure that offers a ready passage to this fluid. This agrees with the idea of M. Descartes, except that I would not, like him, give the pores the shape of round, hollow canals. This is so far from being at all absurd or incomprehensible that it is easily credible that nature uses an infinite series of different-sized molecules in order to produce her marvelous effects.

Moreover, although we do not know the cause of elasticity, we cannot have failed to notice that most bodies possess this characteristic; hence it is not unreasonable to suppose that it is a quality of the minute, invisible particles of the ether. And it is a fact that if one looks for some other method of accounting for the gradual transmission of light, he will have a hard time finding any supposition better suited than elasticity to explain the fact of uniform speed. This [uniform speed] seems to be a necessary assumption, for if the motion slowed down when distributed over a great mass of matter at a far distance from its source, then this great speed would at last be lost. On the other hand, we suppose ether to have the property of elasticity so that its particles regain their shape with equal activity whether struck a hard or gentle blow. Thus the rate at which light would move would remain constant.

Translated from Traité de la Lumière.