Trigonometry
Application of Trigonometry
Ptolemy, Almagest II. 3
Given the length of the longest day, to determine the latitude of a place, and conversely.1
A. Now let it be required, given the length of the longest day, to find the elevation of the pole [i.e., the latitude], that is, arc BZ of the meridian.
On the same figure as before,
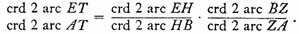
But
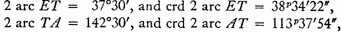
Again,
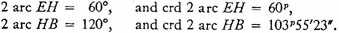
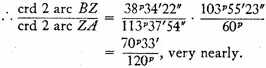
very nearly.
Now
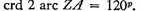
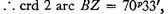
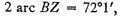
and
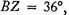
very nearly.
1
B. Now conversely, let arc BZ, representing, on the same figure, the elevation of the pole, be given. Suppose it is determined by observation to be 36°. Let it be required to find the difference between the shortest or longest day and the day of the equinox, i.e., 2 arc ET.
By the same theorem
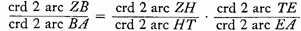
But
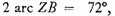
and
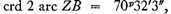
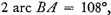 2
2 and
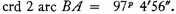
Again,
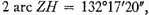 3
3 and

 4
4 and
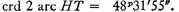
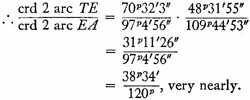
But
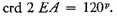
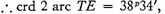
and
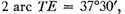
very nearly.
This represents
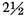
equinoctial hours. Q.E.D.
1
The place Ptolemy has in mind is Rhodes, at approximately 36° north latitude, where the length of the longest day is
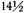
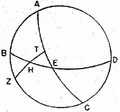
hours. In the accompanying figure
ABCD is the meridian,
BED the horizon,
AEC the equator,
Z a pole,
H the corresponding solstitial point, and
T the point where the great circle through
Z and
H intersects the equator.
ET corresponding to half of
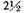
hours, measures 18°45′, and
AT is its complement;
EH has previously been found to be 30°. The equation in both parts is based on Menelaus’s Theorein discussed above, and the computation is performed with the help of the Table of Chords.
1 I.e., a place where the length of the longest day is
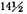
hours is at latitude 36°. The equation, in modern terms, is
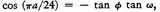
where ø, is the latitude of the place, ω the obliquity of the ecliptic, and
a the length of the longest day in hours. The maximum value of
a in this formula is 24, the length of the longest day at the arctic and antarctic circles. A more complicated formula is necessary for the higher latitudes. The discussion does not take account of (1) the fact that the sun is not a point of light, and (2) the effect of atmospheric refraction in lengthening the time between apparent sunrise and apparent sunset.
2 I.e.,
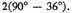
3 I.e.,
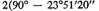
[obliquity of the ecliptic]).
4 I.e., double the obliquity of the ecliptic.