Mechanics

GALILEO

ACCELERATION AND LAVES OF FALLING BODIES

SALV. The present does not seem to be the proper time to investigate the cause of the acceleration of natural motion concerning which various opinions have been expressed by various philosophers, some explaining it by attraction to the center, others to repulsion between the very small parts of the body, while still others attribute it to a certain stress in the surrounding medium which closes in behind the falling body and drives it from one of its positions to another. Now, all these fantasies, and others too, ought to be examined; but it is not really worth while. At present it is the purpose of our Author merely to investigate and to demonstrate some of the properties of accelerated motion (whatever the cause of this acceleration may be)—meaning thereby a motion, such that the momentum of its velocity goes on increasing after departure from rest, in simple proportionality to the time, which is the same as saying that in equal time-intervals the body receives equal increments of velocity; and if we find the properties (of accelerated motion) which will be demonstrated later are realized in freely falling and accelerated bodies, we may conclude that the assumed definition includes such a motion of falling bodies and that their speed goes on increasing as the time and the duration of the motion.

SAGR. So far as I see at present, the definition might have been put a little more clearly perhaps without changing the fundamental idea, namely, uniformly accelerated motion is such that its speed increases in proportion to the space traversed; so that, for example, the speed acquired by a body in falling four cubits would be double that acquired in falling two cubits and this latter speed would be double that acquired in the first cubit. Because there is no doubt but that a heavy body falling from the height of six cubits has, and strikes with, a momentum double that it had at the end of three cubits, triple that which it had at the end of one.

SALV. It is very comforting to me to have had such a companion in error; and moreover let me tell you that your proposition seems so highly probable that our Author himself admitted, when I advanced this opinion to him, that he had for some time shared the same fallacy. But what most surprised me was to see two propositions so inherently probable that they commanded the assent of everyone to whom they were presented, proven in a few simple words to be not only false, but impossible.

SIMP. I am one of those who accept the proposition, and believe that a falling body acquires force in its descent, its velocity increasing in proportion to the space, and that the momentum of the falling body is doubled when it falls from a doubled height; these propositions, it appears to me, ought to be conceded without hesitation or controversy.

SALV. And yet they are as false and impossible as that motion should be completed instantaneously; and here is a very clear demonstration of it. If the velocities are in proportion to the spaces traversed, or to be traversed, then these spaces are traversed in equal intervals of time; if, therefore, the velocity with which the falling body traverses a space of eight feet were double that with which it covered the first four feet (just as the one distance is double the other) then the time-intervals required for these passages would be equal. But for one and the same body to fall eight feet and four feet in the same time is possible only in the case of instantaneous (discontinuous) motion; but observation shows us that the motion of a falling body occupies time, and less of it in covering a distance of four feet than of eight feet; therefore it is not true that its velocity increases in proportion to the space.

The falsity of the other proposition may be shown with equal clearness. For if we consider a single striking body the difference of momentum in its blows can depend only upon difference of velocity; for if the striking body falling from a double height were to deliver a blow of double momentum, it would be necessary for this body to strike with a double velocity; but with this doubled speed it would traverse a doubled space in the same time-interval; observation however shows that the time required for fall from the greater height is longer.

SAGR. You present these recondite matters with too much evidence and ease; this great facility makes them less appreciated than they would be had they been presented in a more abstruse manner. For, in my opinion, people esteem more lightly that knowledge which they acquire with so little labor than that acquired through long and obscure discussion.

SALV. If those who demonstrate with brevity and clearness the fallacy of many popular beliefs were treated with contempt instead of gratitude the injury would be quite bearable; but on the other hand it is very unpleasant and annoying to see men, who claim to be peers of anyone in a certain field of study, take for granted certain conclusions which later are quickly and easily shown by another to be false. I do not describe such a feeling as one of envy, which usually degenerates into hatred and anger against those who discover such fallacies; I would call it a strong desire to maintain old errors, rather than accept newly discovered truths. This desire at times induces them to unite against these truths, although at heart believing in them, merely for the purpose of lowering the esteem in which certain others are held by the unthinking crowd. Indeed, I have heard from our Academician many such fallacies held as true but easily refutable; some of these I have in mind.

SAGR. You must not withhold them from us, but, at the proper time, tell us about them even though an extra session be necessary. But now, continuing the thread of our talk, it would seem that up to the present we have established the definition of uniformly accelerated motion which is expressed as follows:

A motion is said to be equally or uniformly accelerated when, starting from rest, its momentum receives equal increments in equal times.

SALV. This definition established, the Author makes a single assumption, namely,

The speeds acquired by one and the same body moving down planes of different inclinations are equal when the heights of these planes are equal.

By the height of an inclined plane we mean the perpendicular let fall from the upper end of the plane upon the horizontal line drawn through the lower end of the same plane. Thus, to illustrate. let the line AB (Fig. 1) be horizontal, and let the planes CA and CD be inclined to it; then the Author calls the perpendicular CB the "height" of the planes CA and CD; he supposes that the speeds acquired by one and the same body, descending along the planes CA and CD to the terminal points A and D are equal since the heights of these planes are the same, CB; and also it must be understood that this speed is that which would be acquired by the same body falling from C to B.

SAGR. Your assumption appears to me so reasonable that it ought to be conceded without question, provided of course there are no chance or outside resistances, and that the planes are hard and smooth, and that the figure of the moving body is perfectly round, so that neither plane nor moving body is rough. All resistance and opposition having been removed, my reason tells me at once that a heavy and perfectly round ball descending along the lines CA, CD, CB would reach the terminal points A, D, B, with equal momenta.

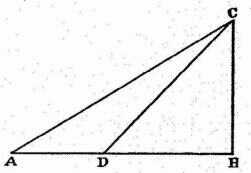FIG. 1.

SALV. Your words are very plausible; but I hope by experiment to increase the probability to an extent which shall be little short of a rigid demonstration.

Imagine this page to represent a vertical wall, with a nail driven into it; and from the nail let there be suspended a lead bullet of

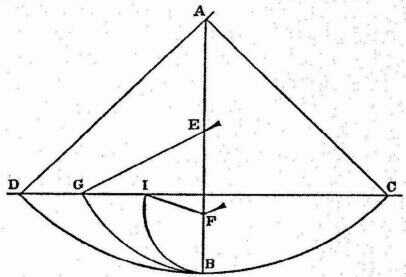FIG. 2.

one or two ounces by means of a fine vertical thread, AB, (Fig. 2) say from four to six feet long, on this wall draw a horizontal line DC, at right angles to the vertical thread AB, which hangs about two finger-breadths in front of the wall. Now bring the thread AB with the attached ball into the position AC and set it free; first it will be observed to descend along the arc CBD, to pass the point B, and to travel along the arc BD, till it almost reaches the horizontal CD, a slight shortage being caused by the resistance of the air and the string; from this we may rightly infer that the ball in its descent through the arc CB acquired a momentum on reaching B, which was just sufficient to carry it through a similar arc BD to the same height. Having repeated this experiment many times, let us now drive a nail into the wail close to the perpendicular AB, say at E or F, so that it projects out some five or six finger-breadths in order that the thread, again carrying the bullet through the arc CB, may strike upon the nail E when the bullet reaches B, and thus compel it to traverse the arc BG, described about E as center. From this we can see what can be done by the same momentum which previously starting at the same point B carried the same body through the are BD to the horizontal CD. Now, gentlemen, you will observe with pleasure that the ball swings to the point G in the horizontal, and you would see the same thing happen if the obstacle were placed at some lower point, say at F, about which the ball would describe the are BI, the rise of the ball always terminating exactly on the line CD. But when the nail is placed so low that the remainder of the thread below it will not reach to the height CD (which would happen if the hall were placed nearer B than to the intersection of AB with the horizontal CD) then the thread leaps over the nail and twists itself about it.

This experiment leaves no room for doubt as to the truth of our supposition; for since the two arcs CB and DB are equal and similarly placed, the momentum acquired by the fall through the arc CB is the same as that gained by fall through the arc DB; but the momentum acquired at B, owing to fall through CB, is able to lift the same body through the arc BD; therefore, the momentum acquired in the fall BD is equal to that which lifts the same body through the same arc from B to D; so, in general, every momentum acquired by fall through an arc is equal to that which can lift the same body through the same arc. But all these momenta which cause a rise through the arcs BD, BG, and BI are equal, since they are produced by the same momentum, gained by fall through CB, as experiment shows. Therefore all the momenta gained by fall through the arcs DB, GB, IB are equal.

SAGR. The argument seems to me so conclusive and the experiment so well adapted to establish the hypothesis that we may, indeed, consider it as demonstrated.

SALV. I do not wish, Sagredo, that we trouble ourselves too much about this matter, since we are going to apply this principle mainly in motions which occur on plane surfaces, and not upon curved, along which acceleration varies in a manner greatly different from that which we have assumed for planes.

So that, although the above experiment shows us that the descent of the moving body through the arc CB confers upon it momentum just sufficient to carry it to the same height through any of the arcs BD, BG, BI, we are not able, by similar means, to show that the event would be identical in the case of a perfectly round ball descending along planes whose inclinations are respectively the same as the chords of these arcs. It seems likely, on the other hand, that, since these planes form angles at the point B, they will present an obstacle to the ball which has descended along the chord CB, and starts to rise along the chord BD, BG, BI.

In striking these planes some of its momentum will be lost and it will not be able to rise to the height of the line CD; but this obstacle, which interferes with the experiment, once removed, it is clear that the momentum (which gains in strength with descent) will be able to carry the body to the same height. Let us then, for the present, take this as a postulate, the absolute truth of which will be established when we find that the inferences from it correspond to and agree perfectly with experiment. The author having assumed this single principle passes next to the propositions which he clearly demonstrates; the first of these is as follows:

Theorem I, Proposition I

The time in which any space is traversed by a body starting from rest and uniformly accelerated is equal to the time in which that same space would be traversed by the same body moving at a uniform speed whose value is the mean of the highest speed and the speed just before acceleration began.

Let us represent by the line AB (Fig. 3) the time in which the space CD is traversed by a body which starts from rest at C and is uniformly accelerated; let the final and highest value of the speed gained during the interval AB be represented by the line EB drawn at right angles to AB; draw the line AE, then all lines drawn from equidistant points on AB and parallel to BE will represent the increasing values of the speed, beginning with the instant A. Let the point F bisect the line EB; draw FG parallel to BA, and GA parallel to FB, thus forming a parallelogram AGFB which will be equal in area to the triangle AEB, since the side GF bisects the side AE at the point I; for if the parallel line in the triangle AEB are extended to GI, then the sum of all the parallels contained in the quadrilateral is equal to the sum of those contained in the triangle AEB; for those in the triangle IEF are equal to those contained in the triangle GIA, while those included in the trapezium AIFB are common. Since each and every instant of time in the time-interval AB has its corresponding point on the line AB, from which points parallels drawn in and limited by the triangle AEB represent the increasing values of the growing velocity, and since parallels contained within the rectangle represent the values of a speed which is not increasing, but constant, it appears, in like manner, that the momenta assumed by the moving body may also be represented, in the case of the accelerated motion, by the increasing parallels of the triangle AEB, and, in the case of the uniform motion, by the parallels of the rectangle GB. For, what the momenta may lack in the first part of the accelerated motion (the deficiency of the momenta being represented by the parallels of the triangle AGI) is made up by the momenta represented by the parallels of the triangle IEF.

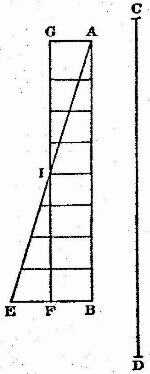FIG. 3.

Hence it is clear that equal spaces will be traversed in equal times by two bodies, one of which, starting from rest, moves with a uniform acceleration, while the momentum of the other, moving with uniform speed, is one-half its maximum momentum under accelerated motion.

Q. E. D.

Theorem II, Proposition II

The spaces described by a body falling from rest with a uniformly accelerated motion are to each other as the squares of the time-intervals employed in traversing these distances.

Let the time beginning with any instant A be represented by the straight line AB (Fig. 4) in which are taken any two time-intervalsAD and AE. Let HI represent the distance through which the body, starting from rest at H, falls with uniform acceleration. If HL represents the space traversed during the time-interval AD, and HM that covered during the interval AE, then the space MH stands to the space LH in a ratio which is the square of the ratio of the time AE to the time AD; or we may say simply that the distances HM and HL are related as the squares of AE and AD.

Draw the line AC making any angle whatever with the line AB; and from the points D and E, draw the parallel lines DO and EP; of these two lines, DO represents the greatest velocity attained during the interval AD, while EP represents the maximum velocity acquired during the interval AE. But it has just been proved that so far as distances traversed are concerned it is precisely the same whether a body falls from rest with a uniform acceleration or whether it falls during an equal time-interval with a constant speed which is one-half the maximum speed attained during the accelerated motion. It follows therefore that the distances HM and HL are the same as would be traversed, during the time-intervals AE and AD, by uniform velocities equal to one-half those represented by DO and EP respectively. If, therefore, one can show that the distances HM and HL are in the same ratio as the squares of the time-intervals AE and AD, our proposition will be proven.

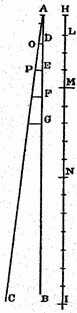FIG. 4.

But in the fourth proposition of the first book it has been shown that the spaces traversed by two particles in uniform motion bear to one another a ratio which is equal to the product of the ratio of the velocities by the ratio of the times. But in this case the ratio of the velocities is the same as the ratio of the time-intervals (for the ratio of AE to AD is the same as that of ½EP to ½DO or of EP to DO). Hence the ratio of the spaces traversed is the same as the squared ratio of the time-intervals.

Q. E. D.

Evidently then the ratio of the distances is the square of the ratio of the final velocities, that is, of the lines EP and DO, since these are to each other as AE to AD.

Corollary I

Hence it is clear that if we take any equal intervals of time whatever, counting from the beginning of the motion, such as AD,DE, EF, FG, in which the spaces HL, LM, MN, NI are traversed, these spaces will bear to one another the same ratio as the series of odd numbers, 1, 3, 5, 7; for this is the ratio of the differences of the squares of the lines (which represent time), differences which exceed one another by equal amounts, this excess being equal to the smallest line (viz. the one representing a single time-interval): or we may say (that this is the ratio) of the differences of the squares of the natural numbers beginning with unity.

While, therefore, during equal intervals of time the velocities increase as the natural numbers, the increments in the distances traversed during these equal time-intervals are to one another as the odd numbers beginning with unity.

SIMP. In truth, I find more pleasure in this simple and clear argument of Sagredo than in the Author’s demonstration which to me appears rather obscure; so that I am convinced that matters are as described, once having accepted the definition of uniformly accelerated motion. But as to whether this acceleration is that which one meets in nature in the case of falling bodies, I am still doubtful; and it seems to me, not only for my own sake but also for all those who think as I do, that this would be the proper moment to introduce one of those experiments—and there are many of them, I understand—which illustrate in several ways the conclusions reached.

SALV. The request which you, as a man of science, make, is a very reasonable one; for this is the custom—and properly so—in those sciences where mathematical demonstrations are applied to natural phenomena, as is seen in the ease of perspective, astronomy, mechanics, music, and others where the principles, once established by well-chosen experiments, become the foundations of the entire superstructure. I hope therefore it will not appear to be a waste of time if we discuss at considerable length this first and most fundamental question upon which hinge numerous consequences of which we have in this book only a small number, placed there by the Author, who has done so much to open a pathway hitherto closed to minds of speculative turn. So far as experiments go they have not been neglected by the Author; and often, in his company, I have attempted in the following manner to assure myself that the acceleration actually experienced by falling bodies is that above described.

A piece of wooden moulding or scantling, about 12 cubits long, half a cubit wide, and three finger-breadths thick, was taken; on its edge was cut a channel a little more than one finger in breadth; having made this groove very straight, smooth, and polished, and having lined it with parchment, also as smooth and polished as possible, we roiled along it a hard, smooth, and very round bronze ball. Having placed this board in a sloping position, by lifting one end some one or two cubits above the other, we roiled the ball, as I was just saying, along the channel, noting, in a manner presently to be described, the time required to make the descent. We repeated this experiment more than once in order to measure the time with an accuracy such that the deviation between two observations never exceeded one-tenth of a pulse-beat. Having performed this operation and having assured ourselves of its reliability, we now roiled the ball only one-quarter the length of the channel; and having measured the time of its descent, we found it precisely one-half of the former. Next we tried other distances, comparing the time for the whole length with that for the half, or with that for two-thirds, or indeed for any fraction; in such experiments, repeated a full hundred times, we always found that the spaces traversed were to each other as the squares of the times, and this was true for all inclinations of the plane, i.e., of the channel, along which we roiled the ball. We also observed that the times of descent, for various inclinations of the plane, bore to one another precisely that ratio which, as we shall see later, the Author had predicted and demonstrated for them.

For the measurement of time, we employed a large vessel of water placed in an elevated position; to the bottom of this vessel was soldered a pipe of small diameter giving a thin jet of water, which we collected in a small glass during the time of each descent, whether for the whole length of the channel or for a part of its length; the water thus collected was weighed, after each descent, on a very accurate balance; the differences and ratios of these weights gave us the differences and ratios of the times, and this with such accuracy that although the operation was repeated many, many times, there was no appreciable discrepancy in the results.

SIMP. I would like to have been present at these experiments; but feeling confidence in the care with which you performed them, and in the fidelity with which you relate them, I am satisfied and accept them as true and valid.

SALV. Then we can proceed without discussion.

Corollary II

Secondly, it follows that, starting from any initial point, if we take any two distances, traversed in any time-interval whatsoever, these time-intervals bear to one another the same ratio as one of the distances to the mean proportional of the two distances.

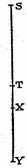FIG. 5.

For if we take two distances ST and SY (Fig. 5) measured from the initial point S, the mean proportional of which is SX, the time of fall through ST is to the time of fall through SY as ST is to SX; or one may say the time of fall through SY is to the time of fall through ST as SY is to SX. Now since it has been shown that the spaces traversed are in the same ratio as the squares of the times; and since, moreover, the ratio of the space SY to the space ST is the square of the ratio SY to SX, it follows that the ratio of the times of fall through SY and ST is the ratio of the respective distances SY and SX.

Scholium

The above corollary has been proven for the case of vertical fall; but it holds also for planes inclined at any angle; for it is to be assumed that along these planes the velocity increases in the same ratio, that is, in proportion to the time, or, if you prefer, as the series of natural numbers.

SALV. Here, Sagredo, I should like, if it be not too tedious to Simplicio, to interrupt for a moment the present discussion in order to make some additions on the basis of what has already been proved and of what mechanical principles we have already learned from our Academician. This addition I make for the better establishment on logical and experimental grounds, of the principle which we have above considered; and what is more important, for the purpose of deriving it geometrically, after first demonstrating a single lemma which is fundamental in the science of motion.

SAGR. If the advance which you propose to make is such as will confirm and fully establish these sciences of motion, I will gladly devote to it any length of time. Indeed, I shall not only be glad to have you proceed, but I beg of you at once to satisfy the curiosity which you have awakened in me concerning your proposition; and I think that Simplicio is of the same mind.

SIMP. Quite right.

SALV. Since then I have your permission, let us first of all consider this notable fact, that the momenta or speeds of one and the same moving body vary with the inclination of the plane.

The speed reaches a maximum along a vertical direction, and for other directions diminishes as the plane diverges from the vertical. Therefore the impetus, ability, energy, or, one might say, the momentum of descent of the moving body is diminished by the plane upon which it is supported and along which it rolls.

For the sake of greater clearness erect the line AB (Fig. 6) perpendicular to the horizontal AC; next draw AD, AE, AF, etc., at different inclinations to the horizontal. Then I say that all the momentum of the falling body is along the vertical and is a maximum when it falls in that direction; the momentum is less along DA and still less along EA, and even less yet along the more inclined plane FA. Finally on the horizontal plane the momentum vanishes altogether; the body finds itself in a condition of indifference as to motion or rest; has no inherent tendency to move in any direction, and offers no resistance to being set in motion. For just as a heavy body or system of bodies cannot of itself move upwards, or recede from the common center toward which all heavy things tend, so it is impossible for any body of its own accord to assume any motion other than one which carries it nearer to the aforesaid common center. Hence, along the horizontal, by which we understand a surface, every point of which is equidistant from this same common center, the body will have no momentum whatever.

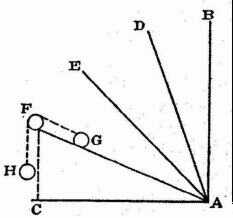FIG. 6.

This change of momentum being dear, it is here necessary for me to explain something which our Academician wrote when in Padua, embodying it in a treatise on mechanics prepared solely for the use of his students, and proving it at length and conclusively when considering the origin and nature of that marvellous machine, the screw. What he proved is the manner in which the momentum varies with the inclination of the plane, as for instance that of the plane FA, one end of which is elevated through a vertical distance FC. This direction FC is that along which the momentum of a heavy body becomes a maximum; let us discover what ratio this momentum bears to that of the same body moving along the inclined plane FA. This ratio, I say, is the inverse of that of the aforesaid lengths. Such is the lemma preceding the theorem which I hope to demonstrate a little later.

It is clear that the impelling force acting on a body in descent is equal to the resistance or least force sufficient to hold it at rest. In order to measure this force and resistance I propose to use the weight of another body. Let us place upon the plane FA a body G connected to the weight H by means of a cord passing over the point F; then the body H will ascend or descend, along the perpendicular, the same distance which the body G ascends or descends along the inclined plane FA; but this distance will not be equal to the rise or fall of G along the vertical in which direction alone G, as other bodies, exerts its force. This is clear. For if we consider the motion of the body G, from A to F, in the triangle AFC to be made up of a horizontal component AC and a vertical component CF, and remember that this body experiences no resistance to motion along the horizontal (because by such a motion the body neither gains nor loses distance from the common center of heavy things) it follows that resistance is met only in consequence of the body rising through the vertical distance CF. Since then the body G in moving from A to F offers resistance only in so far as it rises through the vertical distance CF, while the other body H must fall vertically through the entire distance FA, and since this ratio is maintained whether the motion be large or small, the two bodies being inextensibly connected, we are able to assert positively that, in case of equilibrium (bodies at rest) the momenta, the velocities, or their tendency to motion, i.e., the spaces which would be traversed by them in equal times, must be in the inverse ratio to their weights. This is what has been demonstrated in every case of mechanical motion. So that, in order to hold the weight G at rest, one must give H a weight smaller in the same ratio as the distance CF is smaller than FA. If we do this, FA:FC = weight G:weight H; then equilibrium will occur, that is, the weights H and G will have the same impelling forces, and the two bodies will come to rest.

And since we are agreed that the impetus, energy, momentum or tendency to motion of a moving body is as great as the force or least resistance sufficient to stop it, and since we have found that the weight H is capable of preventing motion in the weight G, it follows that the less weight H whose entire force is along the perpendicular, FC, will be an exact measure of the component of force which the larger weight G exerts along the plane FA. But the measure of the total force on the body G is its own weight, since to prevent its fall it is only necessary to balance it with an equal weight, provided this second weight be free to move vertically; therefore the component of the force of G along the inclined plane FA will bear to the maximum and total force on this same body G along the perpendicular FC the same ratio as the weight H to the weight G. This ratio is, by construction, the same which the height, FC, of the inclined plane bears to the length FA. We have here the lemma which I proposed to demonstrate and which, as you will see, has been assumed by our Author in the second part of the sixth proposition of the present treatise.

SAGR. From what you have shown thus far, it appears to me that one might infer, arguing ex aequali con la proportione perturbata, that the tendencies of one and the same body to move along planes differently inclined, but having the same vertical height, as FA and FI, are to each other inversely as the lengths of the planes.

SALV. Perfectly right. This point established, I pass to the demonstration of the following theorem:

If a body falls freely along smooth planes inclined at any angle whatsoever, but of the same height, the speeds with which it reaches the bottom are the same.

First we must recall the fact that on a plane of any inclination whatever a body starting from rest gains speed or momentum in direct proportion to the time, in agreement with the definition of naturally accelerated motion given by the Author. Hence, as he has shown in the preceding proposition, the distances traversed are proportional to the squares of the times and therefore to the squares of the speeds. The speed relations are here the same as in the motion first studied [i.e. vertical motion], since in each case the gain of speed is proportional to the time.

Let AB (Fig. 7) be an inclined plane whose height above the level BC is AC. As we have seen above, the force impelling a body to fall along the vertical AC is to the force which drives the same body along the inclined plane AB as AB is to AC. On the incline AB, lay off AD a third proportional to AB and AC; then the fore producing motion along AC is to that along AB (i.e., along AD) as the length AC is to the length AD. And therefore the body will traverse the space AD, along the incline AB, in the same time which it would occupy in falling the vertical distance AC, (since the forces are in the same ratio as these distances); also the speed at C is to the speed at D as the distance AC is to the distance AD. But, according to the definition of accelerated motion, the speed at B is to the speed of the same body at D as the time required to traverse AB is to the time required for AD; and, according to the last corollary of the second proposition, the time of passing through the distance AB hears to the time of passing through AD the same ratio as the distance AC (a mean proportional between AB and AD) to AD. Accordingly the two speeds at B and C each bear to the speed at D the same ratio, namely, that of the distances AC and AD; hence they are equal. This is the theorem which I set out to prove.

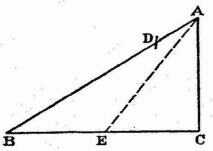FIG. 7.

From the above we are better able to demonstrate the following third proposition of the Author in which he employs the following principle, namely, the time required to traverse an inclined plane is to that required to fall through the vertical height of the plane in the same ratio as the length of the plane to its height.

For, according to the second corollary of the second proposition, if BA represents the time required to pass over the distance BA, the time required to pass the distance AD will be a mean proportional between these two distances and will be represented by the line AC; but if AC represents the time needed to traverse AD it will also represent the time required to fall through the distance AC, since the distances AC and AD are traversed in equal times; consequently if AB represents the time required for AB then AC will represent the time required for AC. Hence the times required to traverse AB and AC are to each other as the distances AB and AC.

In like manner it can be shown that the time required to fall through AC is to the time required for any other incline AE as the length AC is to the length AE; therefore, ex aequali, the time of fall along the incline AB is to that along AE as the distance AB is to the distance AE, etc.

One might by application of this same theorem, as Sagredo will readily see, immediately demonstrate the sixth proposition of the Author; but let us here end this digression which Sagredo has perhaps found rather tedious, though I consider it quite important for the theory of motion.

SAGR. On the contrary it has given me great satisfaction, and indeed I find it necessary for a complete grasp of this principle.

SALV. I will now resume the reading of the text.