Linus Pauling G. W. WHELAND Chemistry

The following selection is from pages 362–365 in The Journal of Chemical Physics 1, 362–374 (1933).

The Nature of the Chemical Bond. V the Quantum Mechanical Calculation of the Resonance Energy of Benzene and Naphthalene and the Hydrocarbon Free Radicals

LINUS PAULING AND G. W. WHELAND

A number of structural formulae have been proposed for benzene, but none of them is free from very serious objections. The oldest

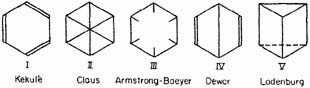
and best known structure is that proposed by Kekulé (I). The objections to it are twofold. First, it suggests that ortho-disubstituted derivatives should exist in two isomeric forms—a phenomenon which has never been observed, Kekulé avoided this difficulty, however, by assuming that the double bonds were in a state of constant oscillations such that any two adjacent carbon atoms were connected part of the time by a single bond and part of the time by a double bond. For example:

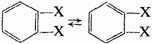
Second, the Kekulé structure suggests that benzene should be a highly unsaturated and comparatively unstable compound, in complete contradiction to the observed facts. Since this point has been discussed in considerable detail in various places, we shall not go into it here. The two centric structures (II and III) were proposed to avoid both of the above difficulties. They are indeed successful in eliminating the necessity for the oscillation hypothesis, but they can hardly account for the stability of the molecule. In the Claus structure the diagonal bonds would be very weak, as a result of the large distance between the atoms in the para positions, and the structure would probably represent a molecule less stable even than the Kekulé structure. In the Armstrong-Baeyer structure the meaning of the six lines pointing toward the center is not at all clear. If these "central bonds" are left undefined, the structure is essentially meaningless; if they are considered to represent free valences, the molecule should be highly unsaturated.

The Dewar structure (IV) has never been seriously considered since it suffers from the same defects, in an accentuated form, as the Kekulé structure. Its advantage over the other structures is largely that it explains the intimate relationship that usually obtains between the para positions in the benzene ring.

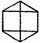
The Ladenburg prism structure (V) can be definitely ruled out, since we know that the benzene ring lies in a plane, or very nearly in a plane. The chemical evidence is also unfavorable in this case.

This by no means exhausts the list of structures proposed for benzene. The remainder however, such as the structure of Thiele based upon his theory of partial valence and that of Collie based upon a dynamic model, are usually complicated and cannot be represented in any simple valence scheme.

In the case of the aromatic hydrocarbons with condensed ring systems that state of affairs is quite similar. Thus the following structures have been proposed for naphthalene:

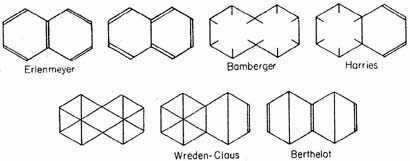
for anthracene:

and so on for the other aromatic hydrocarbons. As in the case of benzene, however, the proposed structures are all unsatisfactory, on account both of the non-occurrence of predicted types of isomerism and of the unexpected stability of the molecules.

Apparently here we have a case where the classical ideas of structural organic chemistry are inadequate to account for the observed properties of a considerable group of compounds. With the development of the quantum mechanics and its application to problems of valence and molecular structure, it became evident to workers in this field that the resonance of benzene between the two equivalent Kekulé structures was an essential feature of the structure of this molecule, accounting for the hexagonal symmetry of the ring and for its remarkable stability; and it seemed probable that the quantum mechanical treatment of aromatic molecules would lead to a completely satisfactory explanation of their existence and characteristic properties. E. Hückel has made a valuable start in this direction in a series of papers on the quantum mechanics of benzene. His method of attack, however, is very cumbersome. In this paper we present a treatment of the problem which is rather closely similar to that of Hückel’s and which leads to the same result in the case of benzene, but in which the calculations are simplified to such an extent that the method can be extended to the naphthalene molecule without undue labor. Furthermore, with the aid of additional simplifications and approximations we have been able to treat the problem of free radicals and to obtain results in surprisingly good qualitative agreement with experiment. We shall leave the discussion of these latter calculations to the second part of the paper.

We shall set up the problem in essentially the same way as Hückel. We assume that each of the six carbon atoms possesses two K electrons, and four L electrons, one for each of four orbital functions formed by linear combination of the 2s and the three 2p orbits. Three of these L orbits, each a combination of the 2s orbit and the two 2p orbits in the plane of the ring, form single bonds to the attached hydrogen atom and the two adjacent carbon atoms. The fourth orbit for each atom remains a pure p-orbit, projecting at right angles to the ring. We neglect the energy of the electrons forming the system of single bonds in the plane and of their interaction with the electrons occupying the pure p-orbits (these energy quantities occurring in the same way for all the structures considered, and hence leading to only a change in the arbitrarily-chosen zero of energy), and consider only the interaction energy of the latter electrons, which may interact with one another in different ways. That is, we treat benzene simply as a six-electron system with spin degeneracy only, and naphthalene as a ten-electron system with spin degeneracy only.

Considerable justification for this choice of orbital functions and of bond distribution is provided by the fact that each of the single exchange integrals between a pure p-orbit and an orbit in the plane of the ring is positive (arising from the e²/r_ij term in the Hamiltonian only), and the chosen distribution of bonds causes these integrals to occur with the negative sign in the expression for the energy of the molecule, while the bonding energy integrals, which are negative, occur with the positive sign.

In carrying out the calculations we make certain further simplifying assumptions. We neglect all exchange integrals of unity, and all exchange integrals of the energy H except single exchange integrals involving two adjacent atoms. The single exchange integrals involving adjacent atoms, (abcdef/H/bacdef), (abcdef/H/acbdef), etc., are represented by the symbol α. These integrals are seen to be equal in benzene; in naphthalene and other aromatic molecules, in which they are not all required to be equal by the symmetry of the molecule, the reasonable assumption is made that no serious error is introduced by giving them all the same value. The Coulomb integral (abcdef/H/abcdef)is represented by the symbol Q.

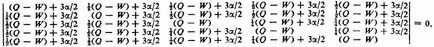
This quintic equation is easily reduced to three linear factors and one quadratic factor, the roots being −2α, −2α, 0,

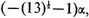
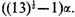
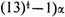
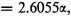
and Since α is negative, the last of these roots, represents the normal state of the molecule. The eigenfunction corresponding to this is (before normalizing)

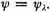
Benzene

The benzene molecule can now be treated very simply by the Slater method, with the help of the rules formulated by one of us for finding the matrix elements occurring in the secular equation. The bonds between the six eigenfunctions can be drawn so as to give the independent canonical structures shown in Fig. 1. Any other structures that can be drawn can be represented by eigenfunctions which are linear combinations of the five above. It will be seen that structures A and B are simply the two Kekulé structures, and C, D, and E

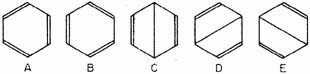Fig. 1. The five canonical structures contributing to the normal state of the benzene molecule.

are three different forms of the Dewar structure. The Claus centric structure does not belong to the canonical set, but it can be represented as a linear combination of canonical structures; and the same is true of the Ladenburg structure if it be considered spread out in a plane, as:

(The Claus structure

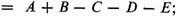
the Ladenburg structure )

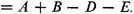
As can be easily verified, the secular equation is

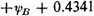
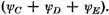
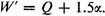
If we had neglected the resonance phenomenon and calculated the energy for one of the structures A or B, we would have obtained the value Hence the extra energy of the molecule resulting from resonance among the five independent structures is 1.1055α. It is interesting to see how much of this extra energy is due to resonance between the two Kekulé structures and how much is contributed by the excited structures C, D and E. A single calculation shows that 0.9α or approximately 80 per cent of the resonance energy comes from the Kekulé structures alone and only about 20 per cent from the three excited structures.

In the following paper of this series a value of about 1.7 v.e. has been found from thermochemical data for the resonance energy of benzene. Equating the negative of this quantity to 1.1055α, we calculate the value of α to be about −1.5 v.e. This value may not be very reliable, however, since it is based on the assumption that values of bond energies obtained from aliphatic compounds can be applied directly to aromatic compounds.

The results of the calculation for benzene are summarized in Table I. They are identical with those obtained by Hückel.

Table I The ratio a:b is the ratio of the coefficient of structures A and B to that of the singly-excited structures C, D, and E.

The conclusions we draw regarding the structure of the normal benzene molecule are the following. The principal contributions to the structure are made by the two Kekulé structures, resonance between them stabilizing the molecule to the extent of 0.9α or about 1.35 v.e. over a ring with three double bonds. In addition, however, the excited structures contribute appreciably to the energy (0.2055α) and to the eigenfunction.¹ In a sense it may be said that all structures based on a plane hexagonal arrangement of the atoms—Kekulé, Dewar, Claus, etc.—play a part, with the Kekulé structures most important. It is the resonance among these structures which imparts to the molecule its peculiar aromatic properties.

These ideas are then applied to naphthalene and free radicals in the remainder of the paper.

¹ The Claus centric structure, an old-quantum-theory analogue of which was suggested several years ago by one of us, is found to make a less important contribution to the normal state of benzene than do the Kekulé structures.