Early Middle Ages

The Latin Encyclopedists

ON THE QUADRIVIUM, OR FOUR MATHEMATICAL SCIENCES

Isidore of Seville

Translated by Ernest Brehaut¹

Revised, expanded, and annotated by Edward Grant

Book III

ON MATHEMATICS

[PREFACE]

Mathematics is called in Latin doctrinalis scientia (that is, a theoretical science). It considers abstract quantity. For that is abstract quantity which we treat by reason alone, separating it by the intellect from the material or from other nonessentials, as for example, equal, unequal, or the like. And there are four sorts of mathematics, namely, arithmetic, geometry, music, and astronomy.³ Arithmetic is the science of quantity numerable in itself. Geometry is the science of magnitude and forms. Music is the science that treats of numbers that are found in sounds. Astronomy is the science that contemplates the courses of the heavenly bodies and their figures, and all the phenomena of the stars. These sciences we shall next describe at a little greater length in order that their significance may be fully shown.⁴

CHAPTER l

ON THE NAME OF THE SCIENCE OF ARITHMETIC

1. Arithmetic is the science of numbers. For the Greeks call number

The writers of secular literature have decided that it is first among the mathematical sciences since it needs no other science for its own existence.

2. But music and geometry and astronomy, which follow, need its aid in order to be and exist.

CHAPTER 2

ON THE WRITERS

1. They say that Pythagoras was the first among the Greeks to write of the science of number, and that it was later described more fully by Nicomachus, whose work Apuleius first, and then Boethius, translated into Latin.⁵

CHAPTER 3

WHAT NUMBER IS

1. Number is multitude made up of units. For one is the seed of number but not number. Nummus (coin) gave its name to numerus (number), and from being frequently used, originated the word.

Unus derives its name from the Greek, for the Greeks call unus

likewise duo, tria, which they call and

2. Quattuor took its name from a square figure (figura quadrata). Quinque, however, received its name from one who gave the names to numbers not according to nature but according to whim. Sex and septem come from the Greek.

3. For in many names that are aspirated in Greek we use s instead of the aspiration. We have sex for

septem for and also the word serpillum (thyme) for herpillum. Octo is borrowed without change; they have we novem; they we decem.

4. Decem is so called from a Greek etymology, because it ties together and unites the numbers below it. For to tie together and unite is called among them

. . . .⁶

CHAPTER 4

WHAT NUMBERS SIGNIFY

1. The science of number must not be despised. For in many passages of the holy scriptures it is manifest what great mystery they contain. For it is not said in vain in the praises of God (Book of Wisdom 11:21): "but thou hast ordered all things in measure, and number, and weight."⁷ For the senarius, which is perfect in respect to its parts,⁸ declares the perfection of the universe by a certain meaning of its number. In like manner, too, the forty days which Moses and Elias and the Lord himself fasted are not understood without an understanding of number.

3. So, too, other numbers appear in the holy scriptures whose nature none but experts in this art can wisely declare the meaning of. It is granted to us, too, to depend in some part upon the science of numbers, since we learn the hours by means of it, reckon the course of the months, and learn the time of the returning year. Through number, indeed, we are instructed in order not to be confounded. Take number from all things and all things perish. Take calculation from the world and all is enveloped in dark ignorance, nor can he who does not know the way to reckon be distinguished from the rest of the animals.

CHAPTER 5

ON THE FIRST DIVISION INTO EVEN AND ODD

1. Number is divided into even and odd. Even number is divided into the following: evenly even, evenly uneven, unevenly even, and unevenly uneven. Odd number is divided into the following: prime and incomposite, composite, and a third intermediate class (mediocris) which in a certain way is prime and incomposite but in another way secondary and composite.

2. An even number is that which can be divided into two equal parts, as II, IV, VIII.⁹ An odd number is that which cannot be divided into equal parts, there being one in the middle which is either too little or too much, as III, V, VII, IX, and so on.

3. Evenly even number is that which is divided equally into even number, until it comes to indivisible unity, as for example, LXIV has a half XXXII, this again XVI; XVI, VIII; eight, IV; four, II; two, one, which is single and indivisible.

4. Evenly uneven is that which admits of division into equal parts, but its parts soon remain indivisible, as VI, X, XXXVIII, and L, for presently, when you divide such a number, you run upon a number which you cannot halve.¹⁰

5. Unevenly even number is that whose halves can be divided again but do not go on to unity, as XXIV. For this number being divided in half makes XII, divided again VI, and again, three; and this part does not admit of further division, but before unity a limit is found which you cannot halve.

6. Unevenly uneven is that which is measured unevenly by an uneven number, as XXV, XLIX; which, being uneven numbers, are divided also by uneven factors, as, seven times seven, XLIX, and five times five, XXV. Of odd numbers some are prime, some composite, some intermediate (mediocris).

7. Simple [or prime] numbers are those which have no other part [or factor] except unity alone, as three has only a third, five only a fifth, seven only a seventh,¹¹ for these have only one factor.

Composite numbers are those which are not only measured by unity, but are produced¹² by another number, as nine, (novem), XV, XXI, [XXV]. For we say three times three (ter terni) [are IX], and seven times three (septies terni) [are XXI], and three times five (ter quini) [are XV], and five times five (quinquies quini) [are XXV].

8. Intermediate (mediocris) numbers are those which in a certain fashion seem prime and incomposite and in another fashion secondary and composite. For example, when nine (novem) is compared with XXV, it is prime and incomposite because it has no common number except the monad [or unit] only; but if it is compared with fifteen (quindecim), it is secondary and composite since there is in it a common number in addition to unity, that is, the number three (because three times three make nine, and three times five make fifteen).

9. Likewise of even numbers some are excessive, others defective, others perfect. Excessive are those whose factors being added together exceed its total, as for example, twelve. For it has five parts [or factors]: a twelfth, which is one; a sixth, which is two; a fourth, which is three; a third, which is four; a half, which is six. For one and two and three and four and six being added together make XVI, which is far in excess of twelve. And there are many similar kinds, as eighteen, and many such.

10. Defective numbers are those which being reckoned by their factors make a less total, as for example, X, which has three parts: a tenth, which is one; a fifth, which is two; and a half, which is five. . . .

11. The perfect number is that which is equaled by its factors, as six, for it has three parts: a sixth, a third, and a half. Now a sixth of it is one, a third is two, a half is three. When these parts are summed—that is, one, two, and three—they perfect and complete the [number] six. The perfect numbers are, under ten, VI; under a hundred, XXVIII; under a thousand, CCCCXCVI.

CHAPTER 6

ON THE SECOND DIVISION OF ALL NUMBER

1. All number is considered either with reference to itself or in relation to something. The former is divided as follows: some are equal; others are unequal. The latter is divided as follows: some are greater, some are less.¹³ The greater are divided as follows: into multiples, superparticulars, superpartients, multiple superparticulars, multiple superpartients.¹⁴ The lesser are divided as follows: submultiples, subsuperparticulars, subsuperpartients, submultiple subsuperparticulars, submultiple subsuperpartients.

2. A number is said to be by itself which is said to be without any relation [or ratio], as III, IV, V, VI, and similar others. A number is related to something which is compared relatively to others, as, for example, IV to II, which is called a double [ratio]; also VI to III, VIII to IV, X to V; and III to one is a triple [ratio, as are] VI to II, IX to III, and so on.¹⁵

3. Those numbers are said to be equal which are equal in quantity, as II to II, III to Ill, X to X, and C to C. Those numbers are unequal which when mutually compared show an inequality, as III to II, IV to III, V to IV, X to VI; and universally, when a greater is compared to a lesser [number] and a lesser to a greater, they are said to be unequal.

4. A number is greater which contains the smaller number to which it is compared [or related] plus something more; for example, number five is greater than number three because number five contains number three and two other parts of it; and so on for others.

5. A smaller number is one that is contained by the greater to which it is compared [or related] plus some part of it, as three to five, for it is contained by it with its two other parts. . . .¹⁶

7. The superparticular number is when a greater number contains in itself a lesser number with which it is compared, and at the same time one part of it.

For example, III when compared with II contains in itself II and also one, which is the half of two. IV when compared with III contains III and also one, which is the third of three. Likewise V when compared with IV contains the number four and also one, which is the fourth part of the said number four,¹⁷ and so on.

8. The superpartient number is that which contains the whole of a lesser number and in addition II parts of it, or III, or IV, or V, or other parts. For example, when V is compared with III, the number five contains three and in addition to this II parts of it. . . .¹⁸

CHAPTER 7

ON THE THIRD DIVISION OF ALL NUMBER

1. Numbers are discrete (discreti) or continuous (continentes).¹⁹ The latter are divided as follows: first, lineal; second, superficial; third, solid. Discrete number is that which is made up of discrete units. For example, III, IV, V, VI, and so on.

2. Continuous number is that which is made up of connected units, as, for example, the number three understood in magnitude, that is, it is said to be continuous in a line or space, or solid; similarly for the numbers four and five.²⁰

3. A lineal number is one that begins from unity and is written lineally to infinity.²¹ For this reason alpha is used to designate lines, since among the Greeks this letter signifies one.

4. A superficial [or plane] number is that which is constituted not only by length but also by breadth, as triangular, square, pentangular, or circular numbers, and the rest that are contained in a plane surface or superficies.²²

5. A circular number is one that has been multiplied by itself; it begins with itself and returns to itself. For example, five times five is XXV.²³ A solid number is one that is contained by length, width, and depth, as are pyramids, which rise in the manner of a flame.

6. Cube numbers are like dice. Spheres are things that are everywhere equal in rotundity. A spherical number is one that has been multiplied from a circular number; it begins from itself and returns to itself. Five times five is XXV. When this circle has been multiplied by itself, it makes a sphere, that is, five times XXV [makes] CXXV.

CHAPTER 8

ON THE DISTINCTION BETWEEN ARITHMETIC, GEOMETRY, AND MUSIC

1. Between arithmetic, geometry, and music there is a difference in finding the means. In the first place, you do as follows in arithmetic. Join [or add] the extremes and divide and you get the mean. For example, let VI and XII be the extremes and you add them and they make [or equal] X and VIII;²⁴ you divide the means²⁵ and get IX, which is the mean of arithmetic (analogicum arithmeticae). Thus the mean exceeds the first term by as many units as it is exceeded by the extreme. For IX exceeds VI by three units and XII exceeds it by three units.

2. According to geometry you find it this way. The extremes multiplied together make as much as the means multiplied (duplicata); for example, VI and XII multiplied make seventy two (septuagies dipondius); the means VIII and IX multiplied make the same.²⁶

3. According to music, you find it this way: the mean exceeds the first term by the same part as the mean is exceeded by the extreme [or last term]. For example, VI, VIII [and XII]; so that the mean [i.e., VIII] exceeds [VI] by two parts, which is one third [of the first term], and the mean is exceeded by the last term [by a third part of it].²⁷

CHAPTER 9

THAT INFINITE NUMBERS EXIST

1. It is most certain that there are infinite numbers, since at whatever number you think an end must be made I say not only that it can be increased by the addition of one, but, however great it is, and however large a multitude it contains, by the very method and science of numbers it can not only be doubled but even multiplied.

2. Each number is limited by its own proper qualities, so that no one of them can be equal to any other. Therefore, in relation to one another they are unequal and diverse, and the separate numbers are each finite, and all are infinite.

CHAPTER 10

ON THE INVENTORS OF GEOMETRY AND ITS NAME

1. The science of geometry is said to have been discovered first by the Egyptians, because when the Nile overflowed and all their lands were overspread with mud, its origin in the division of the land by lines and measurements gave the name to the art. And later, being carried further by the keenness of the philosophers, it measured the spaces of the sea, the heavens, and the air.

2. For, having their attention aroused, students began to search into the spaces of the heavens after measuring the earth; how far the moon was from the earth, the sun itself from the moon, and how great a measure extended to the summit of the sky; and thus they laid off in numbers of stades with probable reason the very distances of the sky and the circuit of the earth.

3. But since this science arose from the measuring of the earth, it took its name also from its beginning. For geometria is so named from "earth" and "measuring." For the earth is called

in Greek, and measuring, The art of this science embraces lines, intervals, magnitudes, and figures; and in figures, dimensions and numbers.

CHAPTER 11

ON THE FOURFOLD DIVISION OF GEOMETRY

1. The fourfold division of geometry is into plane figures, numerable magnitude, rational magnitude, and solid figures.

2. Plane figures are those which are contained by length and breadth, and which are five in number according to Plato.²⁸ Numerable magnitude is that which can be divided by the numbers of arithmetic.

3. Rational magnitudes are those whose measures we can know, and irrational, those the amount of whose measurement is not known.

4. Solid figures are those that are contained by length, breadth, and thickness,²⁹ as [for example], a cube; and there are five species in a plane.³⁰

CHAPTER 12

ON THE FIGURES OF GEOMETRY

1. The first of these, the circle, is a plane figure which is called a circumference, in the middle of which is a point upon which everything converges (cuncta convergunt), which geometers call the center and the Latins call the point of the circle.

2. A quadrilateral figure is a square in a plane which consists of four straight lines, thus.^3l A

dianatheton grammon is a plane figure,³² thus. An orthogonium, that is, a right angle (rectiangulum), is a plane figure, for it is a triangle and has a right angle.³³ The plane figure isopleuros is straight and constructed underneath.³⁴

3. A sphere is a figure of rounded form equal in all its parts.

4. A cube is a proper solid figure which is contained by length, breadth, and thickness.³⁵ A cylinder is a square figure with a semicircle above.³⁶

5. A cone (conon) is a solid figure which narrows from a broad base like a right-angled triangle.³⁷

6. A pyramid is a figure which narrows from a broad base to a point like fire.³⁸ For among the Greeks fire is called

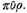
7. Furthermore, just as all number is [contained] below X,³⁹ so is the outline of all figures contained within a circle.⁴⁰ The first figure of this kind is a point, which has no part.⁴¹ The second is a line, which has length besides breadth. A straight line is that which lies evenly in respect to its points. A surface is that which has length and breadth only. Lines are the limits [or boundaries] of surfaces, and the forms [or shapes] in the ten figures mentioned above are not posited because they are found among them.⁴²

CHAPTER 13

ON THE NUMBERS OF GEOMETRY

You investigate numbers according to geometry as follows: The extremes being multiplied (multiplicata) amount to as much as the means multiplied (duplicata);⁴⁴ as for example VI and XII being multiplied make seventy two; the means VIII and IX being multiplied amount to the same.⁴⁵

CHAPTER 15

ON MUSIC AND ITS NAME

1. Music is the practical knowledge of melody, consisting of sound and song; and it is called music by derivation from the Muses. And the Muses were so called

that is, from inquiring, because it was by them, as the ancients had it, that the potency of songs and the melody of the voice were inquired into.

2. Since sound is a thing of sense it passes along into past time, and it is impressed on the memory. From this it was pretended by the poets that the Muses were the daughters of Jupiter and Memory. For unless sounds are held in the memory by man, they perish, because they cannot be written.

CHAPTER 16

ON ITS DISCOVERERS

1. Moses says that the discoverer of the art of music was Jubal, who was of the family of Cain and lived before the flood. But the Greeks say that Pythagoras discovered the beginnings of this art from the sound of hammers and the striking of tense cords. Others assert that Linus of Thebes, and Zethus, and Amphion, were the first to win fame in the musical art.

2. After whose time this science in particular was gradually established and enlarged in many ways, and it was as disgraceful to be ignorant of music as of letters. And it had a place not only at sacred rites but at all ceremonies and in all things glad or sorrowful.

CHAPTER 18

ON THE THREE PARTS OF MUSIC

1. There are three parts of music, namely, harmonica, rhythmica, metrica. Harmonica is that which distinguishes in sounds the high and the low. Rhythmica is that which inquires concerning the succession of words as to whether the sound fits them well or ill.

2. Metrica is that which learns by approved method the measure of the different meters, as, for example, the heroic, iambic, elegiac, and so on.

CHAPTER 19

ON THE TRIPLE DIVISION OF MUSIC

1. It is agreed that all sound which is the material of music is of three sorts. First is harmonica, which consists of vocal music; second is organics, which is formed from the breath; third is rhythmica, which receives its numbers from the beat of the fingers.

2. For sound is produced either by the voice, coming through the throat; or by the breath, coming through the trumpet or tibia, for example; or by touch, as in the case of the cithara or anything else that gives a tuneful sound on being struck.

CHAPTER 20

ON THE FIRST DIVISION OF MUSIC, WHICH IS CALLED HARMONICA

1. The first division of music, which is called harmonica, that is, modulation of the voice, has to do with comedians, tragedians, and choruses, and all who sing with the proper voice. This [coming] from the spirit and the body makes motion, and out of motion, sound, out of which music is formed, which is called in man the voice. . . .

2. Harmonica is the modulation of the voice and the concord or fitting together of very many sounds.

3. Symphonia is the managing of modulation so that high and low tones accord, whether in the voice or in wind or stringed instruments. Through this, higher and lower voices harmonize, so that whoever makes a dissonance from it offends the sense of hearing. The opposite of this is diaphonia, that is, voices grating on one another or in dissonance.

7. Tonus is a high utterance of voice. For it is a difference and measure of harmony which depends on the stress and pitch of the voice. Musicians have divided its kinds into fifteen parts, of which the hyperlydian is the last and highest, the hypodorian the lowest of all.⁴⁷

8. Song is the modulation of the voice, for sound is unmodulated, and sound precedes song. . . .

CHAPTER 21

ON THE SECOND DIVISION, WHICH IS CALLED ORGANICA

1. The second division, organics, has to do with those [instruments] that, filled with currents of breath, are animated so as to sound like the voice, as for example, trumpets, reeds, Pan’s pipes, organs the pandura, and instruments like these. . . .⁴⁸

CHAPTER 22

ON THE THIRD DIVISION, WHICH IS CALLED RHYTHMICA

1. The third division is rhythmica, having to do with strings and instruments that are beaten, to which are assigned the different species of cithara, the drum, and the cymbal, the sistrum, acitabula of bronze and silver, and others of metallic stiffness that when struck return a pleasant tinkling sound, and the rest of this sort.

2. . . . The form of the cithara in the beginning is said to have been like the human breast, because as the voice was uttered from the breast so was music from the cithara, and it was so called for the same reason. For pectus is in the Doric language called

. . .

CHAPTER 23

ON THE NUMBERS OF MUSIC

1. You inquire into numbers according to music as follows: Setting down the extremes, as, for example, VI and twelve, you see by how many units VI is surpassed by XII, and it is by VI units; you square it; six times six make XXXVI. You add those first-mentioned extremes, VI and XII; together they make XVIII; you divide thirty-six by eighteen; two is the result. This you add to the smaller amount, six namely; the result will be VIII and it will be a mean between VI and XII. Because VIII surpasses VI by two units, that is by a third of VI, and VIII is surpassed by XII by four units, a third part [of twelve]. By what part, then, the mean surpasses, by the same is it surpassed.⁴⁹

2. Just as this proportion exists in the universe, being constituted by the revolving circles, so also in the microcosm—not to speak of the voice—it has such great power that man does not exist without harmony. . . .

CHAPTER 24

ON THE NAME OF ASTRONOMY

1. Astronomy is the law of the stars, and it traces with inquiring reason the courses of the heavenly bodies, and their figures, and the regular movements of the stars with reference to one another and to the earth.

CHAPTER 25

ON ITS DISCOVERERS

1. The Egyptians were the first to discover astronomy (astronomia). And the Chaldeans first taught astrology (astrologia)⁵⁰ and the observance of nativity. Moreover, Josephus asserts⁵¹ that Abraham taught astrology to the Egyptians. The Greeks, however, say that this art was first elaborated by Atlas, and therefore it was said that he held the heavens up.

2. Whoever was the discoverer, it was the movement of the heavens and his rational faculty that stirred him, and in the light of the succession of seasons, the observed and established courses of the stars, and the regularity of the intervals, he considered carefully certain dimensions and numbers, and by limiting and distinguishing them he wove them into order and discovered astrology.

CHAPTER 26

ON ITS TEACHERS

1. In both Greek and Latin there are volumes written on astronomy by different writers. Of these Ptolemy, King of Alexandria,⁵² is considered chief among the Greeks. He also formulated rules (canones) by which the courses of the stars may be discovered.

CHAPTER 27

THE DIFFERENCE BETWEEN ASTRONOMY AND ASTROLOGY

1. There is some difference between astronomy and astrology. For astronomy embraces the revolution of the heavens, the rising, setting, and motion of the heavenly bodies, and the origin of their names. Astrology, on the other hand, is in part natural, in part superstitious.

2. It is natural astrology when it describes the courses of the sun and the moon or the fixed positions of the stars and the times (seasons?). Superstitious astrology is that which the mathematici follow who prophesy by the stars and who distribute the twelve signs of the heavens among the individual parts of the soul or body and endeavor to predict the nativities and characters of men from the course of the stars.

CHAPTER 28

ON THE SUBJECT MATTER OF ASTRONOMY

1. The subject matter of astronomy is made up of many kinds. For it defines what the universe is, the heavens, the position and movement of the sphere, the axis of the heavens and the poles, what are the climates of the heavens, what the courses of the sun and moon and stars, and so forth.

CHAPTER 29

ON THE UNIVERSE AND ITS NAME

1. Mundus (the universe) is that which is made up of the heavens and earth and the sea and all the heavenly bodies. And it is called mundus for the reason that it is always in motion (motus).⁵³ For no repose is granted to its elements.

CHAPTER 30

ON THE FORM OF THE UNIVERSE

1. The form of the universe is described as follows: As the universe is raised toward the region of the north, so it is inclined toward the south; its head and face are, as it were, the east, and its extreme part the north.

CHAPTER 31

ON THE HEAVENS AND THEIR NAME

1. The philosophers have asserted that the heavens are round, in rapid motion, and made of fire, and that they are called by this name (coelum) because they have the forms of the stars fixed on them, like a dish with figures in relief (coelatum).

2. For God decked them with bright lights, and filled them with the glowing orbs of the sun and moon, and adorned them with the glittering images of flashing stars. . . .⁵⁵

CHAPTER 32

ON THE SITUATION OF THE CELESTIAL SPHERE

1. The sphere of the heavens is rounded and its center is the earth, equally shut in on every side. This sphere, they say, has neither beginning nor end, for the reason that being rounded like a circle it is not easily perceived where it begins or where it ends.⁵⁶

2. The philosophers have brought in the theory. of seven heavens of the universe, that is, planets moving with the harmony of the spheres, and they assert that all planets are connected to their orbs, and they think that these, being connected and, as it were, fitted to one another, move backward and are borne with definite motions in contrary directions.

CHAPTER 33

ON THE MOTION OF THE SAME SPHERE

1. The sphere revolves on two axes, of which one is the northern, which never sets, and is called Boreas; the other is the southern, which is never seen, and is called Austronotius.

2. On these two poles the sphere of heaven moves, they say, and with its motion the stars fixed in it pass from the east all the way around to the west, with the northern stars near the pole (iuxta cardinem) describing smaller circles.

CHAPTER 34

ON THE COURSE OF THE SAME SPHERE

1. The sphere of heaven, [moving] from the east towards the west, turns once in a day and night, in the space of twenty-four hours, within which the sun completes his swift revolving course over and under the earth.

CHAPTER 35

ON THE SWIFTNESS OF THE HEAVENS

1. With such swiftness is the sphere of heaven said to run, that if the planets (astra) did not run against its headlong course in order to delay it, it would destroy the universe.⁵⁷

CHAPTER 36

ON THE AXIS OF THE HEAVENS

1. The axis is a straight line north which passes through the center of the globe of the sphere and is called axis because the sphere revolves on it like a wheel, or it may be because the Wain is there.

CHAPTER 37

ON THE POLES OF THE HEAVENS

1. The poles are little circles which run on the axis. Of these one is the northern, which never sets and is called Boreas; the other is the southern, which is never seen and is called Austronotius. . . .

CHAPTER 38

ON THE CARDINES OF THE HEAVENS

1. The cardines of the heavens are the ends of the axis and are called cardines (hinges) because the heavens turn on them or because they turn like the heart (cor).⁵⁸

CHAPTER 40

ON THE GATES OF THE HEAVENS

1. There are two gates of the heavens, the east and the west. For by one the sun appears, by the other he retires.

CHAPTER 42

ON THE FOUR PARTS OF THE HEAVENS

1. The climata of the heavens, that is, the tracts or parts, are four, of which the first part is the eastern, where some stars rise; the second, the western, where some stars set; the third, the northern, where the sun comes in the longer days; the fourth, the southern, where the sun comes in the time of the longer nights.⁵⁹

4. There are also other climata of the heavens, seven in number, as if seven lines from east to west, under which the manners of men are dissimilar and animals of different species appear; they are named from certain famous places, of which the first is Meroe; the second, Syene; the third, Catachoras, that is Africa; the fourth, Rhodus; the fifth, Hellespontus; the sixth, Mesopontus; the seventh, Boristhenes.⁶⁰

CHAPTER 43

ON THE HEMISPHERES

1. A hemisphere is half a sphere. The hemisphere above the earth is that part of the heavens the whole of which is seen by us; the hemisphere under the earth is that which cannot be seen as long as it is under the earth.

CHAPTER 44

ON THE FIVE CIRCLES OF THE HEAVENS

1. There are five zones in the heavens, according to the differences of which certain parts of the earth are inhabitable because of their moderate temperature and certain parts are uninhabitable because of extremes of heat and cold. And these are called zones or circles for the reason that they exist on the circumference of the sphere.

2. The first of these circles is called

[the Arctic] because the constellations of the north are seen enclosed within it; the second is called [i.e., summer], which is called [i.e., summer tropic], because in this circle the sun makes summer in northern regions and does not pass beyond it but immediately returns.

3. The third circle is called

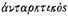
which is equivalent to equinoctialis in Latin, for the reason that when the sun comes to this circle it makes equal day and night. For means in Latin day equal to the night, and by this circle the sphere is seen to be equally divided. The fourth circle is called [antarctic] for the reason that it is opposite to the circle which we call Arctic.

4. The fifth circle is called the

[i. e., winter tropic, or tropic of Capricorn],⁶¹ which in Latin is hiemalis or brumalis, because when the sun comes to this circle it makes winter for those who are in the north and summer for those who dwell in the parts of the south.

CHAPTER 47

ON THE SIZE OF THE SUN

1. The size of the sun is greater than that of the earth, and so from the moment when it rises it appears equally to east and west at the same time. And as to its appearing to us about a cubit in width, it is necessary to reflect how far the sun is from the earth, which distance causes it to seem small to us.

CHAPTER 48

ON THE SIZE OF THE MOON

1. The size of the moon also is said to be less than that of the sun. For while the sun is higher than the moon and still appears to us larger than the moon, if it should approach near to us it would be plainly seen to be much larger than the moon. Just as the sun is larger than the earth, so the earth is in some degree larger than the moon.

CHAPTER 49

ON THE NATURE OF THE SUN

1. The sun, being made of fire, heats to a whiter glow because of the excessive speed of its circular motion. And its fire, philosophers declare, is fed with water, and it receives the virtue of light and heat from an element opposed to it. Whence we see that it is often wet and dewy.

CHAPTER 50

ON THE MOTION OF THE SUN

1. They say that the sun has a motion of its own and does not turn with the universe. For if it remained fixed in the heavens all days and nights would be equal, but since we see that it will set tomorrow in a different place from where it set yesterday, it is plain that it has a motion of its own and does not move with the universe. For it accomplishes its yearly orbits by unequal distances on account of the changes of the seasons (temporum mutationes).⁶²

2. For going further to the south, it makes winter, in order that the land may be enriched by winter rains and frosts. Approaching the north, it restores the summer, in order that fruits may mature and what is green in the damp weather may ripen in the heat.

CHAPTER 52

ON THE JOURNEY OF THE SUN

1. The rising sun makes a journey to the meridian; and after it comes to the west and has bathed itself in ocean, it passes by unknown ways beneath the earth and again returns to the east.

CHAPTER 53

ON THE LIGHT OF THE MOON

1. Certain philosophers hold that the moon has a light of its own, that one part of its globe is bright and another dark, and that, turning by degrees, it assumes different shapes. Others, on the contrary, assert that the moon has no light of its own but is illumined by the rays of the sun. And therefore it suffers an eclipse if the shadow of the earth is interposed between itself and the sun. For the sun is farther than it. Hence when the moon is under it [i.e., between earth and sun], the sun lights the farther [or upper] part of the moon, and the nearer [or lower] part, which it holds toward the earth, would be darker.

CHAPTER 56

ON THE MOTION OF THE MOON

1. The moon governs the measures of the months by alternately losing and recovering its light. It advances in its path obliquely, not directly as the sun, lest it should appear in the center of the earth’s [shadow] and frequently suffer eclipse.⁶³ For its orbit is near the earth. The waxing moon has its horns looking east; the waning, west: rightly, because it is going to set and lose its light.

CHAPTER 57

ON THE NEARNESS OF THE MOON TO THE EARTH

1. The moon is nearer the earth than is the sun. Therefore, with a smaller orb, it finishes its course more quickly. For it traverses in thirty days the journey the sun accomplishes in three hundred and sixty-five. Whence the ancients made the months depend on the moon, the years on the course of the sun.

CHAPTER 58

ON THE ECLIPSE OF THE SUN

1. There is an eclipse of the sun as often as the thirtieth moon reaches the same line where the sun is passing, and, interposing itself, darkens the sun. For it seems that the sun disappears to us when the moon’s orb is opposed to it.

CHAPTER 59

ON THE ECLIPSE OF THE MOON

1. There is an eclipse of the moon as often as the moon runs into the shadow of the earth. For it is thought to have no light of its own but to be illumined by the sun, whence it suffers eclipse if the shadow of the earth comes between it and the sun. The fifteenth moon suffers this until it passes out from the center and shadow of the interposing earth and sees the sun and is seen by the sun.

CHAPTER 61

ON THE LIGHT OF THE STARS

1. Stars are said to have no light of their own, but to be lighted by the sun like the moon.

CHAPTER 62

ON THE POSITION OF THE STARS

1. Stars are motionless, and being fixed, are carried along by the heavens in perpetual course, and they do not set by day but are obscured by the brilliance of the sun.

CHAPTER 63

ON THE COURSES OF THE STARS

1. Stars either are borne along or have motion. Those are borne along which are fixed in the heavens and revolve with the heavens. Certain have motion, like the planets, that is, the wandering stars, which go through roaming courses, but with definite limitations.

CHAPTER 64

ON THE VARYING COURSES OF THE STARS

1. According as stars are carried on different orbs of the heavenly planets, certain ones rise earlier and set later, and certain rising later, come to their setting earlier. Others rise together and do not set at the same time. But all in their own time revolve in a course of their own.

CHAPTER 65

ON THE DISTANCES OF THE STARS

1. Stars are at different distances from the earth and therefore, being of unequal brightness, they are more or less plain to the sight; many are larger than the bright ones which we see, but being further away they appear small to us.⁶⁴

CHAPTER 66

ON THE CIRCULAR NUMBER OF THE STARS

1. There is a circular number of the stars by which it is said to be known in what time each and every star finishes its orbit, whether in longitude or latitude.

2. For the moon is said to complete its orbit every year, Mercury in twenty, Lucifer in nine, the sun in nineteen, Vesper in fifteen, Phaeton in twelve, Saturn in thirty.⁶⁵ When these are finished, they return to a repetition of their orbits through the same constellations and regions.⁶⁶

CHAPTER 67

ON THE WANDERING STARS

1. Certain stars are called planetae, that is, wandering, because they hasten around through the whole universe with varying motions. Because they wander or produce irregularities, they are called retrograde; that is, when they add and subtract little bits. When they subtract so much of the rest, they are said to be retrograde; when, however, they stand [or rest], they make a station.⁶⁷

CHAPTER 68

ON THE PRECEDING [MOTION] OF STARS

1. Praecedentia or antegradatio of stars is when a star seems to be making its usual course and [really] is somewhat ahead of it.

CHAPTER 69

1. Remotio or retrogradatio of stars is when a star, while moving on its regular orbit, seems at the same time to be moving backward.

CHAPTER 70

1. The status of stars means that while a star is continuing its proper motion it nevertheless seems in some places to stand still.

CHAPTER 71

ON THE NAMES OF STARS

3. Stellae is derived from stare, because the stars always remain (stant) fixed in the heavens and do not fall. As to our seeing stars fall, as it were, from heaven, they are not stars but little bits of fire that have fallen from the ether, and this happens when the wind, blowing high, carries along with it fire from the ether, which as it is carried along gives the appearance of falling stars. For stars cannot fall; they are motionless (as has been said above) and are fixed in the heavens and carried around with them.

16. A comet is so called because it spreads light from itself as it if were hair (comas). And when this kind of star appears it indicates pestilence, famine, or war.

17. Comets are called in Latin crinitae because they have a trail of flames resembling hair (in modum crinium). The Stoics say there are over thirty of them, and certain astrologers have written down their names and qualities. . . .⁶⁸

^1. The selection below is drawn from Isidore of Seville’s Etymologies (Etymologiae), Book III, as translated in Ernest Brehaut, An Encyclopedist of the Dark Ages (New York: Columbia University Press, 1912), pp. 125–152. Brehaut’s volume consists of a series of extracts from a few of the twenty books of Isidore of Seville’s Etymologies, written toward the end of Isidore’s life (he died in 636). Since Brehaut’s translation is frequently inaccurate and distorted, I have corrected it freely, using the later Latin edition of W. M. Lindsay (see n. 3) and have also translated a number of passages that Brehaut omitted, often without indication.

^2. William H. Stahl, Roman Science (Madison, Wis.: University of Wisconsin Press, 1962), p. 216.

^3. These four mathematical sciences were customarily designated as the quadrivium and formed the scientific part of the traditional seven liberal arts. The remaining three, called the trivium, consisted of grammar, rhetoric, and dialectic (or logic). The concept of seven liberal arts—that is, artes liberales, studies fit for a free man as opposed to a slave—can be traced to the Greeks as far back as the fourth century B.C. It was Martianus Capella (fl. 410–439), however, in his tremendously influential book The Marriage of Mercury and Philology, who canonized the seven liberal arts for the Latin medieval tradition. Isidore is but following this tradition, which he also helps to establish.

It should be noted that Brehaut’s translation was made from DuBreul’s edition of Isidore’s works published in Paris in 1601. In the more recent two-volume edition of the Etymologies (Oxford: Clarendon Press, 1911) by W. M. Lindsay, music appears before geometry in this sentence and is described immediately after arithmetic a few sentences below. Such trivial differences will be ignored.

^4. The substance, and sometimes the very words, of this paragraph were taken from Cassiodorus’ section "On Mathematics" in his An Introduction to Divine and Human Readings, translated by L. W. Jones (New York: Columbia University Press, 1946), pp. 178–179. Almost all of what Isidore writes on arithmetic was taken from Cassiodorus, who in turn drew largely upon Boethius’ Arithmetic.

^5. This paragraph is drawn directly from Cassiodorus (see Jones, p. 187).

^6. In the next few lines Isidore gives etymological derivations for 20, 30, 100, 200, 1,000, and thousands.

^7. I have replaced the Latin text of this Biblical quotation with the English translation from the Douay version. This quotation was widely cited as justification for the study of mathematics.

^8. Six was considered a perfect number because it equals the sum of all its factors.

^9. In Lindsay’s Latin edition of the Etymologies, Roman and rhetorical numerals are used indiscriminately. To convey a sense of this inconsistency, I have expressed all numbers as they appear in the text.

^10. According to Cassiodorus, an "evenly uneven" (Jones renders it as "even-times-odd") number "is one whose similar division into two equal parts can occur but once; for example, 10, whose half is 5. . ." (Jones, p. 181). Although Isidore’s examples agree with this definition, he fails to restrict his version to a single division.

^11. Here Isidore has slightly altered and made more cumbersome the remark of Cassiodorus, who says merely that a prime number "is one which can be divided by unity alone; for example, 3, 5, 7, 11, 13, 17, and the like" (Jones, p. 182). Isidore, however, speaks of 1/3 of 3 as the factor of 3; 1/5 of 5, and so on.

^12. Cassiodorus properly says that such numbers can be divided by unity and another number. But Isidore says obscurely that they can also be "produced" (procreantur) by another number.

^13. Isidore is actually referring to ratios. Thus if

where A and B are numbers, then A/B is a ratio of greater inequality and B/A one of lesser inequality.

^14. Since only the superparticular and superpartient ratios are discussed below, I shall cite Isidore’s examples for the others:

(1) Multiple ratios: 2/1, 3/1, 4/1; the respective submultiples are 1/2, 1/3, 1/4, That is, n/1 and 1/n respectively, where n is any integer.

(2) Multiple superparticular ratios: 5/2 and 9/4 where the greater term contains the lesser an integral number of times plus a unit fractional part. The respective submultiples are 2/5 and 4/9, In general,

where m and n are greater than l and all terms are integers; the reciprocal will represent the submultiples.

(3) Multiple superpartient ratios: 8/3, 14/6, 16/7, 21/9, where the greater term contains the lesser an integral number of times plus a proper fraction reduced to its lowest terms. Thus, although Isidore includes 14/6 and 21/9, these do not qualify, since

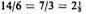
and which converts them to superparticular ratios. The respective submultiple superpartients would be 3/8, 7/16. Generally, one may represent multiple superpartient ratios by where P is an integer greater than or equal to 1 and m and n are mutually prime integers greater than 1 and

^15. I have translated and added this paragraph and paragraphs 3–5.

^16. For the remainder of chapter 6, Isidore provides descriptions and examples of the five types of ratios of greater and lesser inequality enumerated in paragraph 1 of this sixth chapter. Only the sections on superparti-cular and superpartient ratios of greater inequality are translated here (for the rest, see n. 14). All five types of ratios were drawn from Cassiodorus, who derived them from the Arithmetic of Boethius.

^17. The subsuperparticulars of these respective examples are 2/3, 3/4, 4/5. Generally

where represents any superparticular; in each case the reciprocal provides the submultiple.

^18. Any superpartient ratio can be represented by

where m and n are mutually prime integers greater than 1 and Once again, the reciprocal of any superpartient ratio represents its subsuperpartient. Although in his brief summary Isidore refers to multiple, superparticular, and superpartient numbers, it is ratios that are meant, since in all cases we have a relation between two numbers.

^19. I have altered Brehaut’s translation from "abstract or concrete" to "discrete or continuous." These changes have been made systematically in the rest of the chapter; other changes have also been required by Brehaut’s misunderstanding of the chapter; I have also added the translation of paragraph 3 and some lines omitted in other paragraphs.

^20. Cassiodorus, from whom Isidore drew the last two paragraphs, says (Jones, p. 185): "A continuous number is one which consists of connected units; as 3, for example, would be called continuous if it was understood to be the measurement of a magnitude, that is, the measurement era line or a space or a solid; the same applies to 4 and to 5."

^21. In commenting on this passage as it appears in Cassiodorus and from whence Isidore derived it, Jones observes (p. 185, n. 20), "Unity is not included, for a line is the aggregate of two or more points. 2, 3, 4, 5, 6, etc., are linear numbers."

^22. As examples of superficial numbers Isidore gives a triangular number, a square number, and a pentagonal number, which were apparently represented by appropriate figures in the manuscripts but were omitted in the Latin edition by Lindsay. Cassiodorus, from whom Isidore derived all this, provided diagrams for these figurate numbers (see Jones, p. 180) but supplied no additional descriptive information. From Nicomachus and Boethius, however, it is apparent that a triangular number is represented by

so that if then the successive triangular numbers are 1, 3, 6, 10, 15, . . . , where 6, for example, is the sum of and could be thought of in the triangular arrangement.

Fig. 1

The successive square numbers may be represented generally as n² where

and n is the side of each square. Pentagonal numbers consist of the sequence 1, 5, 12, 22, 35, . . . and in general where

^23. Thus

is circular, became after the original number is multiplied by itself it terminates with itself; the same applies to

^24. Although it is unclear, Isidore may have intended to use some or all of the terms 12, 10, 8, and 6 to illustrate the three kinds of means. However, the text of the musical mean seems corrupt and the numbers used cannot be exactly determined.

^25. Here Isidore divides the sum of 10 and 8, which ale means between 12 and 6.

^26. Isidore has utterly confused the geometric mean, for although he offers an acceptable definition, his example does not illustrate the definition. A geometric mean is represented as

so that but after inserting means 8 and 9 between extremes 6and 12, Isidore multiplies and believes that he has found a geometric mean! In his chapter 13, Isidore repeats this example.

^27. Brehaut’s translation and Lindsay’s Latin—which differ substantively—do not offer an example of a musical or harmonic mean. Either the text is corrupt or Isidore failed to understand the meaning of musical mean. In the example that I have substituted, the three terms are 6, 8, and 12 such that

and generally Thus 12 exceeds 8 by 4, which is 1/3 of 12; and 6 is less than 8 by 2, which is 1/3 of 6. Hence the difference between each extreme and the mean is 1/3 of that extreme. In Lindsay’s Latin text Isidore gives only numbers 6 and 8 and says that the last term exceeds 8 by a ninth ("VII[I] superatur ab ultima nona")! I have added 12 because it seems that Isidore wished to present his examples with two or more of the series of numbers 12, 10, 8, and 6. This gains plausibility from the fact that in his section on music Isidore repeats an example of a harmonic mean using the numbers 6, 8, and 12. See Isidore’s chapter 23 and my note 49. For Boethius’ discussion of the three types of proportions or means, see Selection 2, chs. 43–47.

^28. It is probable that Isidore has corrupted the five regular solids, which Plato discusses in Timaeus 53C–55C, into five types of plane figure.

^29. Up to this point Isidore has taken the substance of his geometry from Cassiodorus (see Jones, p. 198). Since Cassiodorus has little more than this, Isidore could not have derived the rest of this geometrical section from him.

^30. The text seems defective at this point. It is unclear whether Isidore intended to declare here that there are five species of solid figures in a plane(!) or whether, after completing his definition of solid figure and having exemplified it by the cube, he wishes now to take up the five species of plane figure mentioned in paragraph 2.

^31. Here again Isidore equates a genus of geometric figure, namely four-sided figure, with a particular type of four-sided figure, a square. Here and elsewhere in this chapter, figures were to be inserted. Lindsay’s text does not contain them.

^32. The figure intended here is unclear to me

^33. Isidore seems to equate right angle with triangle and to commit the same error mentioned above in note 31.

^34. Because Isidore’s meaning is so obscure, I present the Latin: "Isopleuros figura plana, recta et subter constituta."

^35. This definition fails to distinguish a cube from any other kind of solid and is identical with Isidore’s definition of solid figures given in his chapter 11, paragraph 4. In Elements XIII, Definition 25, Euclid defines it as follows: "A cube is a solid figure contained by six equal squares." The translation is that of Thomas L. Heath, The Thirteen Books of Euclid’s Elements, 2d ed. (New York: Dover, 1956), III, 261.

^36. How Isidore obtained or arrived at this incredible definition is a mystery. Perhaps it was suggested upon observing the following kind of two-dimensional representation of a cylinder:

Fig. 2

Or perhaps in some manner this is a distortion of Euclid’s definition of cylinder (Elements XI, Def. 21): "When, one side of those about the right angle in a rectangular parallelogram remaining fixed, the parallelogram is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a cylinder" (Heath p. 262). Although the "rectangular parallelogram" may have been distorted to a square, it is difficult to see how the semicircle on the square could have been extracted from this.

^37. Compare Euclid’s definition (Elements XIII, Def. 18): "When, one side of those about the right angle in a right-angled triangle remaining fixed, the triangle is carried round and restored again to the same position from which it began to be moved, the figure so comprehended is a cone" (Heath, p. 262).

^38. It is again instructive to compare Euclid’s definition (Elements XIII, Def. 12): "A pyramid is a solid figure, contained by planes, which is constructed from one plane to one point" (Heath, p. 262).

^39. Isidore probably means that all numbers can be generated from the numbers 1 through 9.

^40. Here Isidore simply means that these figures can be inscribed in a circle. For the solid figures, however, a sphere is required.

^41. I fail to see how this sentence relates to what has immediately preceded. Brehaut solved the problem by omitting "The first figure of this kind is. . ." and convetting the rest to "A point is that which has no part." Thus, the embarrassment of designating a point as a particular kind of figure is avoided.

^42. Isidore’s meaning is wholly unclear. Are the shapes of the figures not mentioned because, for Isidore, they are all inscribed in circles? The point is hardly worth further discussion.

^43. Brehaut calls this chapter 14; but in this I follow Lindsay’s text.

^44. Ordinarily duplieata means "squared" but this translation would invalidate Isidore’s example, which involves the multiplication of two unequal means. Note that Isidore used multiplicata, the proper term in this context, at the beginning of the sentence.

^45. The same example, with the same terminology, was used earlier in chapter 8, paragraph 2, of the discussion on arithmetic. Chapter 14, the last in the section on geometry, has been omitted. It consists of a paragraph briefly describing additional figures. Thus we conclude this frequently incomprehensible and pitiful remnant of Euclidean geometry.

^46. Isidore derives much of this from Cassiodorus’ Introduction to Divine and Human Readings; Secular Letters, chapter V, "On Music" (Jones, pp. 189–196). The discussion of music in the Etymologies is almost wholly nonmathematical (in contrast to Boethius’ On Music). Cassiodorus, but not Isidore, enters into a discussion of fifteen Greek tones.

^47. For this paragraph, Cassiodorus served as Isidore’s source.

^48. Brehaut notes that the pandura was not a wind but a stringed instrument.

^49. Here we have an harmonic mean involving the numbers 6, 8, and 12. See Isidore’s chapter 8, paragraph 3, and my note 27.

^50. Isidore uses the Latin terms astronomia and astrologia much as we would use their English equivalents (see his chapter 27). However, through much of the later Middle Ages, the two terms were used interchangeably and without meaningful distinction.

^51. Cassiodorus, who cites Josephus (Antiquities, Bk. I, ch. 9), is Isidore’s source for this remark. See An Introduction to Divine and Human Readings; Secular Letters (Jones, p. 179).

^52. Isidore has confused Claudius Ptolemy, the Greek astronomer of the second century A.D. and author of the Almagest, with the Greek dynasty of Ptolemaic kings who ruled in Egypt from around 304 B.C. to 30 B.C. (see a selection by Claudius Ptolemy in the section on Cosmology, and a short biography of him at the end of this source book.

^53. As indicated by the title (Etymologies), Isidore is frequently interested in showing the origin of words, motivated by the belief that such knowledge conveys an insight into subject matter. Almost all are false and forced, as is mundus from motus.

^54. Chapter 30 is almost a verbatim repetition of Isidore’s words in his earlier work On the Nature of Things (De natura rerum), chapter 9, "On the World." Since the earlier work is exclusively concerned with astronomy, cosmology, and natural phenomena in the upper regions of air and fire (for example, he considers thunder, lightning, rain, clouds), Isidore draws heavily upon it in the Etymologies. Indeed, the section on astronomy in the Etymologies often seems a highly abbreviated version of the De natura rerum. The latter treatise has been edited and translated into French by Jacques Fontaine, Isidore de Seville Traité de la Nature (Bordeaux: Féret et Fils, 1960).

^55. One sentence involving the derivation of the Greek word for heavens, ouranos, is omitted.

^56. Here again, Isidore forms this chapter by repeating, almost verbatim, a few lines from chapter 12, paragraph 4, of his earlier De natura rerum (see Fontaine, p. 219).

^57. The periodic motion of the planets from west to east in a contrary direction to the daily motion of the heavens from east to west slows the great velocity of the daily motion and prevents the destruction of the heavens.

^58. In what sense cardines turn like a heart is wholly unclear.

^59. Isidore uses the term climata in two different senses, both of which derive from Greek antiquity. Here he employs it to represent the four directions of the celestial sphere, a usage which can be found in Cleomedes’ treatise On the Circular Motion of the Heavenly Bodies, chapter 9, and in Strabo’s Geography (see D. R. Dicks, The Geographical Fragments of Hippaechus [London: University of London, 1960], pp. 155–156). The more usual sense of climata is discussed in the next paragraph and in the next note.

^60. The seven climata mentioned here agree with the seven distinguished by the Greeks except that the latter have Lower Egypt in place of Isidore’s Catachoras. The seven climata were apparently introduced late (probably in the second century B.C.) and only because "they happened to be the seven parallels which passed through the best-known regions of the inhabited world" (Dicks, p. 157). Originally "the

were narrow belts or strips of land on either side of a parallel of latitude; inhabitants of the same clima were assumed to be situated in the same geographical latitude, since, for practical purposes, the celestial phenomena, lengths of the longest and shortest days, and general climatic conditions did not change appreciably within the clima. . ." (Dicks, p. 154). Writers like Polybius and Strabo came to use the term in a broader sense to represent a district or region of the inhabited world (Dicks, p. 156). Eventually "the word lost its original scientific meaning and acquired the broader one of ’region’ or ’district’, but the names of the seven best known parallels were perpetuated" (Dicks, p. 158). In Almagest, Book II, chapter 13, Ptolemy drew up tables based upon the seven climata using the synonymous terms and to designate them, a practice which most ancient writers followed. Pliny (Natural History, VI, 212–220) also described seven circles or parallels which, however, were based on astrological rather than geographical criteria (Dicks, p. 157).

^61. Obviously, the fourth and fifth circles should be reversed. Isidore repeats this very same order of circles in Book XIII (On he World and Its Parts), chapter 6. This is surprising, since he seems to have ordered them correctly in his earlier work On the Nature of Things (De natura rerum), where chapter 10 is titled "On the Five Circles of the World." In the latter treatise, however, Isidore arranges the circles according to the fingers of the hand, seemingly as if these circles were in a single plane. In neither treatise does Isidore identify the zones as lying between two circles, or a pole and a circle; rather he identifies one zone with one circle, rendering his account unclear. Here is my translation of the relevant passage in On the Nature of Things, chapter 10 (translated from Fontaine, p. 209):

"In their definition of the world the philosophers have five circles (which the Greeks call parallels, i.e., zones) into which the orb of the earth is divided. In the Georgics, Virgil shows these, saying: "The sky has five zones" [Georgics I, 233—Ed.] But let us fix them in the manner of our right hand so that our thumb is the arctic circle, [which is] uninhabitable because of cold; the second [finger] is the summer (therinos) circle, [which is] temperate and habitable; the middle [finger] is the equinoctial (isomerinos) circle, [which is] torrid and uninhabitable; the fourth [finger] is the winter (xeimerinos) circle, [which is] temperate and habitable; the smallest [finger] is the antarctic circle, [which is] frigid and uninhabitable.

"2. The first of these is the north circle, the second the solstitial circle [i.e., tropic of Cancer], the third the equinoctial circle [i.e., equator], the fourth is the winter circle [i.e., tropic of Capricorn], and the fifth is the south circle [i.e., antarctic circle]."

Despite Isidore’s arrangement of the circles in the same plane, it is not likely that he thought the earth flat. He was simply confused.

^62. Since the lengths of the seasons are unequal and the sun’s motion is always assumed to be uniform, it follows that the distances, which represent each of the four parts of the sun’s annual orbit and which correspond to the four seasons, would be unequal.

^63. Isidore is here referring to the obliquity of the lunar and solar orbits. If they were in the same plane, eclipses would occur frequently.

^64. Here Isidore appears to assume that the stars are at different distances from the earth, a position that seems incongruous with the notion of a stellar sphere in which the stars are embedded. Only if the sphere of fixed stars was thought to be of enormous thickness could one suppose that stars of varying sizes were scattered about between its widely separated concentric surfaces.

^65. In this strange passage Lucifer is Venus, Phaeton is Jupiter, and Vesper, which means evening star, must signify Mars (probably Pyroeis, the Greek name for Mars, was intended), although it was a name used for Venus. Aside from twelve years for Jupiter and thirty for Saturn, which are their respective sidereal periods, it is wholly unclear what orbital phenomena Isidore thought he was representing with his other data.

^66. Paragraph 3, which consists of a few lines and concludes chapter 66, has been omitted.

^67. This opaque description is improved somewhat in chapter 69. For a discussion of retrogradations and stations see Selection 64.

^68. The remainder of chapter 71, the final chapter of Book III, contains approximately two more pages on how various celestial bodies and divisions received their names.