Motion in a Hypothetical Void

3. Galileo Galilei: His Earliest Law of Motion and His Arguments for Finite Velocity in a Void

Translated and annotated by I. E. Drabkin;⁴⁶ additional notes by Edward Grant⁴⁷

CHAPTER [10]

IN WHICH, IN OPPOSITION TO ARISTOTLE, IT IS PROVED THAT, IF THERE WERE A VOID, MOTION IN IT WOULD NOT TAKE PLACE INSTANTANEOUSLY, BUT IN TIME.

Aristotle, in Book 4 of the Physics, in his attempt to deny the existence of a void adduces many arguments. Those that are found beginning with section 64⁴⁸ are drawn from a consideration of motion. For since he assumes that motion cannot take place instantaneously, he tries to show that, if a void existed, motion in it would take place instantaneoulsy; and, since that is impossible, he concludes necessarily that a void is also impossible. But, since we are dealing with motion, we have decided to inquire whether it is true that, if a void existed, motion in it would take place instantaneously. And since our conclusion will be that motion in a void takes place in time,⁴⁹ we shall first examine the contrary view and Aristotle’s arguments.

In the first place, of the arguments adduced by

Aristotle there is none that involves a necessary conclusion, but there is one which, at first sight, seems to lead to such a conclusion. This is the argument set forth in sections 71 and 72,⁵⁰ in which Aristotle deduces the following inconsistency—that, on the assumption that motion can take place in time in a void, then the same body will move in the same time in a plenum and in a void. In order to be better able to refute this argument, we have decided to state it at this point.

Thus, Aristotle’s first assumption, when he saw that the same body moved more swiftly through the rarer than through the denser medium, was this: that the ratio of the speed of motion in one medium to the speed in the second medium is equal to the ratio of the rareness of the first medium to the rareness of the second. He then reasoned as follows. Suppose body a traverses medium b in time c, and that it traverses a medium rarer than b, namely d, in time e. Clearly, the ratio of time c to time e is equal to the ratio of the density of b to the density of d. Suppose, then, that there is a void f and that body a traverses f, if it is possible, not in an instant, but in time g. And suppose that the ratio of the density of medium d to the density of some new medium is equal to the ratio of time e to time g. Then, front what has been established, body a will move through the new medium in time g, since [the density of] medium d has to that of the new medium the same ratio as time e to time g. But in the same time g body a also moves through the void f. Therefore a will in the same time move over two equal paths, one a plenum, the other a void. But this is impossible. Therefore the body will not move through the void in time; and therefore the motion will be instantaneous.

Such is Aristotle’s proof. And, indeed, his conclusions would have been sound and necessary, if he had proved his assumptions, or at least if these assumptions, even though unproved, had been true. But he was deceived in this, that he assumed as well-recognized axioms propositions which not only are not obvious to the senses, but have never been proved, and cannot be proved because they are completely false. For he assumed that the ratio of the speeds of the same body moving in different media is equal to the ratio of the rarenesses of the media. But that this is false has been fully proved above.⁵¹ In support of that proof, I shall add only this. Suppose it is true that the ratio of the rareness of air to the rareness of water is equal to the ratio of the speed of a body moving in air to the speed of the same body in water. Then, when a drop or some other quantity of water falls swiftly in air, but does not fall at all in water, since the speed in air has no ratio to the speed in water, it follows, according to Aristotle himself, that there will be no ratio between the rareness of air and the rareness of water. But that is ridiculous.⁵²

Therefore, it is clear that, when Aristotle argues in this way, we must answer him as follows. In the first place, as has been shown above, it is not true that differences in the slowness and speed of a given body arise from the greater or lesser density and rareness of the medium. But even if that were conceded, it is still not true that the ratio of the speeds of the motion of the body is equal to the ratio of the rarenesses of the media.

And as for Aristotle’s statement in the same section that it is impossible for one number to have the same relation⁵³ to another number as a number has to zero, this is, of course, true of geometric ratios [viz., a/b], and not merely in numbers but in every kind of quantity. Since, in the case of geometric ratios, it is necessarily true that the smaller magnitude can be added to itself a sufficient number of times so that it will ultimately exceed any magnitude whatever, it follows that this smaller magnitude is something, and not zero. For zero, no matter how often it is added to itself, will exceed no quantity. But Aristotle’s conclusion does not apply to arithmetic relations [viz., the difference

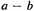
]. That is, in these cases, one number can have the same relation to another number as still another number has to zero. For, since [two pairs of] numbers are in the same arithmetic relation when the difference of the [two] larger is equal to the difference of the [two] smaller,⁵⁴ it will, of course, be possible for one number to have the same [arithmetic] relation to another number, as still another number has to zero. Thus, we say that the [arithmetic] relation of 20 to 12 is the same as that of 8 to 0: for the excess of 20 over 12, i.e., 8, is equal to the excess of 8 over 0.

Therefore, if, as Aristotle held, the ratio of the speeds were equal to the ratio, in the geometric sense, of the rarenesses of the media, Aristotle’s conclusion would have been valid, that motion in a void could not take place in time. For the ratio of the time in the plenum to the time in the void cannot be equal to the ratio of the rareness of the plenum to the rareness of the void,⁵⁵ since the rareness of the void does not exist.⁵⁶ But if the ratio of the speeds were made to depend on the aforesaid ratio, not in the geometric, but in the arithmetic sense [i.e., as a ratio of differences], no absurd conclusion would follow. And, in fact, the ratio of the speeds does depend, in an arithmetic sense, on the relation of the lightness of the first medium to that of the second. For the ratio of the speeds is equal, not to the ratio of the lightness of the first medium to that of the second, but, as has been proved, to the ratio of the excess of the weight of the body over the weight of the first medium to the excess of the weight of the body over the weight of the second medium.

So that this may be clearer, here is an example. Suppose there is a body a whose weight is 20, and two media unequal in weight, bc and de. Let the volume of b be equal to that of a, and the volume of d also equal to that of a. Since we are now discussing downward motion that takes place in a void, let the media be lighter than the body a, and let the weight of b be 12, and of d 6. It is clear, then, from what was proved above, that the ratio of the speed of body a in medium bc to the speed of the same body in medium de will be equal to the ratio of the excess of the weight of a over the weight of b to the excess of the weight of a over the weight of d, that is, as 8 is to 14. Thus if the speed of a in medium bc is 8, its speed in medium de would be 14. Now it is clear that the ratio of the speeds, 14 to 8, is not the same as the ratio (in the geometric sense) of the lightness of one medium to the lightness of the other. For the lightness of medium de is double that of medium bc (for since the weight of b is 12, and of d 6, i.e., since the weight of b is double the weight of d, the lightness of d will be double the lightness of b); but a speed of 14 is less than twice a speed of 8. Yet the speed 14 has to the speed 8 the same relation, in the arithmetic sense, as the lightness of d to the lightness of b, since the difference between 14 and 8 is 6, and 6 is also the difference between the lightness of d (12) and the lightness of b (6).⁵⁷

Furthermore, if medium de should be lighter, so that the weight of d is 5, the speed f will be 15 (for 15 will be the difference between the weight of body a and the weight of the medium d). And again the relation [i.e., arithmetic difference] of speed 15 and speed 8 will be the same as between the weight of medium b (12) and the weight of medium d (5), that is, the same as the relation of the lightness of d and the lightness of b. For the difference in each case will be 7. Furthermore, if the weight of d is only 4, the speed f will be 16: and the relation of speed 16 and speed 8 (with a difference of 8) is the same arithmetic relation as between the weight of b (12) and the weight of d (4), i.e., between the lightness of d and the lightness of b, the difference being also 8. If, again, medium de becomes lighter, and the weight of d is only 3, the speed f will now be 17. And between the speed f (17) and the speed 8 (a difference of 9), the difference is the same as between the weight of b (12) and the weight of d (3), i.e., as between the lightness of d and the lightness of b. If, again, medium de becomes lighter, and the weight of d is only 2, the speed f will now be 18. And the arithmetic difference between that speed and the speed 8 will be the same as the difference between the weight of b (12) and the weight of d (2), i.e., between the lightness of d and the lightness of b. In each case the difference will be 10. If, again, medium de becomes lighter, and the weight of d is only 1, the speed f will now be 19. And there will be the same arithmetic difference between this speed and the speed 8 as between the weight of

b (12) and the weight of d (1), i.e., between the lightness of d and the lightness of b. In each case the difference will be 11. Now if, finally, the weight of d is 0, so that the difference between the weight of body a and of the medium d is 20, the speed f will be 20; and the arithmetic difference between the speed f (20) and the speed 8 will be the same as that between the weight of b (12) and the weight of d (0), the difference in each case being 12.

It is clear, therefore, that the relation of speed to speed is the same as the relation of the lightness of one medium to the lightness of the other, not geometrically [i.e., as a quotient] but arithmetically [i.e., as a difference]. And since it is not absurd for this arithmetic relation [i.e., difference] to be the same between one quantity and a second quantity as between a third quantity and zero, it will similarly not be absurd for the relation of speed to speed to be the same, in this arithmetic sense, as the relation of a given lightness [of medium] to zero.

Therefore, the body will move in a void in the same way as in a plenum. For in a plenum the speed of motion of a body depends on the difference between its weight and the weight of the medium through which it moves. And likewise in a void [the speed of] its motion will depend on the difference between its own weight and that of the medium.⁵⁸ But since the latter is zero, the difference between the weight of the body and the weight of the void will be the whole weight of the body. And therefore the speed of its motion [in the void] will depend on its own total weight.⁵⁹ But in no plenum will it be able to move so quickly, since the excess of the weight of the body over the weight of the medium is less than the whole weight of the body. Therefore its speed will be less than if it moved according to its own total weight.

From this it can clearly be understood that in a plenum, such as that which surrounds us, things do not weigh their proper and natural weight, but they will always be lighter to the extent that they are in a heavier medium. Indeed, a body will be lighter by an amount equal to the weight, in a void, of a volume of the medium equal to the volume of the body. Thus, a lead sphere will be lighter in water than in a void by an amount equal to the weight, in a void, of an aqueous sphere of the same size as the lead sphere. And the lead sphere is lighter in air than in a void by an amount equal to the weight, in a void, of a sphere of air having the same size as the lead sphere. And so also in fire, and in other media. And since the speed of a body’s motion depends on the weight the body has in the medium in which it moves, its motion will be swifter, the heavier the body is in relation to the various media.

But the following argument is invalid: "A void is a medium infinitely lighter than every plenum; therefore motion in it will be infinitely swifter than in a plenum; therefore such motion will be instantaneous." For it is true that a void is infinitely lighter than any [nonvacuous] medium; but we must not say that such a [nonvacuous] medium is of infinite weight. We must instead understand [the applicability of the term "infinite"] in this way, that between the lightness of air, for example, and a void there may exist an unlimited number of media lighter than air and heavier than a void. And if we understand the matter in this way, there may also exist, between the speed in air and the speed in a void, an unlimited number of speeds, greater than the speed in air and less than the speed in a void. And so also between the weight of a body in air and its weight in a void, an unlimited number of intermediate weights may exist, greater than the weight of the body in air, but less than its weight in a void.

And the same is true of every continuum. Thus between lines a and b, of which a is greater, an unlimited number of intermediate lines, smaller than a, but greater than b may exist (for since the amount by which a exceeds b is also a line, it will be infinitely divisible). But we must not say that line a is infinitely greater than line b, in the sense that even if b were to be added to itself without limit, it would not produce a line greater than a. And by similar reasoning, if we suppose a to be the speed in a void, and b the speed in air, an unlimited number of speeds, greater than b and smaller than a, will be able to exist between a and b. Yet we must not conclude that a is infinitely greater than b, in the sense that the time in which [the motion with] speed a is accomplished, when added to itself any number of times without limit, can still never exceed the time corresponding to speed b, and that, therefore, the speed corresponding to time a is instantaneous.

It is therefore clear how the argument is to be understood. "The lightness of a void infinitely exceeds the lightness of a [nonvacuous] medium; therefore the speed in the void will infinitely exceed the speed in a plenum." All that is conceded. What is denied is the conclusion: "Therefore the speed [i.e., the motion] in the void will be instantaneous." For such motion can take place in time, but in a shorter time than the time corresponding to the speed in a plenum; so that between the time in the plenum and the time in the void an unlimited number of times, greater than the latter and smaller than the former, may exist. Hence it follows, not that motion in a void is instantaneous, but that it takes place in less time than the time of motion in any plenum.

Therefore, to put it briefly, my whole point is this. Suppose there is a heavy body a, whose proper and natural weight⁶⁰ is 1000. Its weight in any plenum whatever will be less than 1000, and therefore the speed of its motion in any plenum will be less than 1000. Thus if we assume a medium such that the weight of a volume of it equal to the volume of a is only 1, then the weight of a in this medium will be 999. Therefore its speed too will be 999. And the speed of a will be 1000 only in a medium in which its weight is 1000, and that will be nowhere except in a void.

This is the refutation of Aristotle’s argument. And from this refutation it can readily be seen that motion in a void does not have to be instantaneous. The other arguments of Aristotle are without force or cogency. To say, for example, that in a void the body will not move in one direction rather than in another, or up rather than down, because the void does not give way upward or downward but equally in all directions,⁶¹ is childish. For I could say the same thing about air. That is, when a stone is in air, how does the air give way downward rather than upward, or to the left rather than to the right, if the rareness of the air is everywhere the same? At this point someone, quoting Aristotle,⁶² might say that air has weight in its own place and therefore helps downward motion more. We shall examine these fantasies in the next chapter, where we shall investigate whether elements have weight in their own proper places. And similarly, when they say that in a void there is neither up nor down, who dreamt this up? If the air were a void, would not the void near the earth be nearer the center than the void which is near [the region of] fire?

Similarly lacking in force is the argument which Aristotle makes about projectiles when he says:⁶³ "Projectiles cannot move in a void, for projectiles, when they have left the hand of the thrower, are moved by the air or by some other corporeal medium that surrounds them and is set in motion. But this is not present in a void." For Aristotle assumes that projectiles are carried along by the medium; and in the proper place we shall show that this is false. And what he adds to his argument, about different bodies moving in the same medium, is also false. For he assumes that in a plenum heavier bodies move more swiftly because they cleave the medium more forcibly, and that this is the only reason for their speed; but since that resistance is not present in a void, he supposes that all motions in a void will take place in the same time and with the same speed—and this, he asserts, is impossible.⁶⁴

Now, in the first place, Aristotle errs in that he does not prove that it is absurd for different bodies to move in a void with the same speed. But he makes an even greater error when he assumes that the speeds of different bodies depend on an ability of heavier bodies to divide the medium better. For, as we showed above, the speed of moving bodies does not depend on this, but on the size of the difference between the weight of the bodies and the weight of the medium. For the speeds are in the ratio of these differences. But the difference between the weights of different bodies and the weight of the same medium is not the same (for otherwise the bodies would be equally heavy). Therefore the speeds will not be equal. For example, in the case of a body whose weight is 8, the excess over the weight of the void (which is 0) is 8; hence its speed will be 8. But if the weight of a body is 4, the excess over the [weight of the] void will, in the same way, be 4; and hence its speed will be 4. Finally, using the same method of proof in the case of the void as we used in the case of the plenum,⁶⁵ we can show that bodies of the same material but of different size move with the same speed in a void. So much for that.

Such⁶⁶ is the force of truth that learned men, even Peripatetics, have recognized that Aristotle’s view on this subject was mistaken, though none of them could properly refute his arguments. And, as for what is contained in Physics 4.71–72,⁶⁷ certainly no one was ever able to refute that argument, for up to now the fallacy in it has never been noticed. And though Scotus, Saint Thomas, Philoponus,⁶⁸ and some others hold a view opposed to Aristotle’s, they arrive at the truth by belief rather than real proof or by refuting Aristotle.⁶⁹ And, indeed, if one were to accept Aristotle’s assumption about the ratio of the speeds of the same body moving in different media, one could scarcely hope to be able to refute Aristotle and upset his proof. For Aristotle assumes that the speed in one medium is to the speed in the other, as the rareness of the first medium is to the rareness of the second. And no one up to now has ventured to deny this relation.⁷⁰

Nor is there any validity in the assumption made by the aforesaid writers, namely, a twofold resistance to the motion of the body—one external, resulting from the density of the medium, the other internal, by reason of the determinate weight of the body.⁷¹ For there is something artificial about this; since those two resistances do not, if we look at the matter carefully, differ from each other. For, as has been made clear above, the density or (to use a better term) the weight of the medium makes for lightness of the moving body, and the lightness of the medium is responsible for the heaviness of the body; and the same body is now heavier, now lighter, according as it is in a lighter or heavier medium.⁷² And so, these writers add nothing new when they assume this twofold resistance, since it is merely increased or decreased according to the decrease or increase⁷³ in the heaviness or density of the medium. But if, on the other hand, they admit that the resistance increases or decreases in the ratio in which the weights of the medium vary, their attempts to upset Aristotle’s argument will be in vain.

^46. [Reprinted with permission of the Regents of the University of Wisconsin from Galileo Galilei "On Motion" and "On Mechanics" Comprising "De Motu" (ca. 1590), translated with Introduction and Notes by I. E. Drabkin, and "Le Meccaniche" (ca. 1600), translated with Introduction and Notes by Stillman Drake (Madison, Wis.: University of Wisconsin Press, 1960), pp. 41–50. Although possibly the earliest extant scientific essay by Galileo, it was left unpublished. It reveals an interesting mixture of traditional (that is, medieval) and new concepts.—Ed.]

^47. [Since additional notes are interspersed with Drabkin’s, the numbers of the notes as they appear in his translation have been altered. Four simple marginal figures, which contribute in no way to the understanding of the arguments, have been omitted.—Ed.]

^48. [214b. 10ff. I have replaced Drabkin’s citation of 214a.27ff., since it does not correspond to Galileo’s reference to Text 64 of Book IV of Aristotle’s Physics. Here, and in other places below, Galileo is using the traditional medieval system of reference to the texts of Aristotle. In all such cases Drabkin has converted the medieval citation to the modern system of reference based upon Bekker numbers.—Ed.]

^49. [As Galileo seems to have acknowledged (see n. 69), this viewpoint was widely adopted in the Middle Ages and, as already stated, is traceable to Avempace and ultimately to Philoponus. See Selection 44.2 and n. 17 thereto.—Ed.]

^50. [215a.24—216a.3. Drabkin gives 215b–216a, which does not precisely embrace Texts 71 and 72.—Ed.]

^51. [In chapter 8. In the next few lines, Galileo describes Aristotle’s law in terms of the rareness, or subtlety, of media, that is,

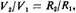
where R is the rareness of a medium. See Selection 44.2, n. 7.—Ed.]

^52. There is the following marginal addition at this point: "If this were true, the ratio of the speed of motion in air to the speed of motion in water would be the same for all bodies. Hence the ratio of the speed of lead in air to its speed in water would be the same as the ratio of the speed of wood in air to its speed in water. But who cannot see that this is false? For lead sinks in water, wood does not."

^53. Galileo’s point depends on two senses of this word (proportio). Aristotle’s conclusion is sound for what Galileo here calls a geometric proportio (i.e., the ratio a/b), but not for an arithmetic proportio (i.e., the difference

).

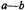
^54. Or, what is equivalent, the difference between the two members of each pair is equal.

^55. There seems to be a slip here. Galileo may have meant to say "density" instead of "rareness" (see the next note). The same effect would have been achieved by saying "ratio of the rareness of the void to the rareness of the plenum" or by speaking of the ratio of speeds, not of times.

^56. In the sense of being greater than any finite number. But Galileo may have meant to speak of density, in which case nulla would be "zero."

^57. If the weights of d and b are 6 and 12, respectively, Galileo here speaks of their lightnesses as 12 and 6, respectively, with difference 6. And similarly in what follows.

^58. [Galileo’s law of motion is

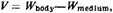
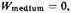
where V is velocity and W is weight per unit volume, or specific weight. Hence a difference in specific weights determines velocity, so that it does not matter whether a body fails in a plenum or a void. The subtractive relation is such that when velocity is proportional to the specific weight of the body. In this Galileo is apparently following the tradition stemming from Avempace (and beyond him probably to Philoponus; for references, see n. 49), where velocity was thought to be determined by the difference—not the ratio as Aristotle would have it—between the weight of a body and the resistance of the medium through which it fell. Resistance of a medium was something to be subtracted, since it served only to retard motion. In the absence of a resistant medium bodies were held to fall freely in the void with a natural finite velocity. Although numbers were arbitrarily assigned and subtractions made (see Bradwardine’s criticism of the first erroneous theory at the beginning of Selection 51.1), to my knowledge no one in the Middle Ages, Avempace included, specified how this subtraction could be interpreted physically. This is not surprising when one realizes that it was usual to conceive of bodies in terms of gross, or total, weight and the resistance of a medium by its density (often vaguely understood). Under these circumstances, no proper subtraction was possible. By utilizing specific weight as the criterion for measuring the difference between body and medium, Galileo, and Giovanni Benedetti before him, made Avempace’s law theoretically precise and intelligible even though it was as erroneous as the dynamic theories with which it contended.—Ed.]

^59. I.e., its weight in the void, undiminished by any weight of medium.

^60. I.e., its weight in a void.

^61. Cf. Physics 215a.22–24.

^62. Cf. De Caelo 311b.9.

^63. Cf. Physics 215a.14–19.

^64.Physics 216a. 12–21.

^65. [For Galileo’s proof, see section 6 below.—Ed.]

^66. This section to the end of the chapter is on a separate sheet. Galileo merely indicated that it belongs in this chapter; and Favaro [the editor of the National Edition of Galileo’s works—Ed.] placed it at the end of the chapter.

^67. [215a.24—216a.3. Drabkin repeats the numbers cited in note 50.—Ed.]

^68. Ioannes Duns Scotus, Opera Omnia III (Paris, 1891), 102–3 (on Arist. Phys. 4. Quaest 12.18,19); D. Thomas Aquinas, Opera III (Rome, 1884), 186. Comm. on Arist. Phys. IV. ch.8. lectio 12, no. 8; Ioannes Philoponus, Comm. in Phys. Arist., pp. 678–84 (Vitelli).

^69. [Duns Scotus, Aquinas, Philoponus, and Avempace (the last-named is mentioned in note 72) are cited because they held, in opposition to Aristotle, that bodies would move in a hypothetical void with finite, not instantaneous, velocities. None of these authors, however, held or asserted Galileo’s other conclusion, namely that homogeneous bodies would fall with equal speed in the void. But a view similar to Galileo’s was held by Thomas Bradwardine (see Theorem XII, Selection 51.1) and Albert of Saxony (see section 2 above, Question 12), and very likely by others.—Ed.]

^70. But Philoponus, cited above by Galileo, does deny the relation as it is expressed in the form "time required in one medium is to the time required in the other medium as density of first medium is to density of the second." Cf. Commentary on Aristotle’s Physics, p. 682.30–32 (Vitelli). [This section from Philoponus is translated in M. R. Cohen and I. E. Drabkin, A Source Book in Greek Science (Cambridge, Mass.: Harvard University Press, 1948), p. 219; Avempace, whom Galileo does not mention in this connection, agreed with Philoponus on this point.—Ed.] G. B. Benedetti also denies the relation (Diversarum speculationum mathematicarum et physicarum liber [Turin, 1585], p. 172; see A. Koyré, Études Galiléennes, I, 50). From what Galileo says one may question how much direct and detailed knowledge he had, at this time, of either Philoponus’ or Benedetti’s work. [The remainder of this note is omitted.—Ed.]

^71. [The internal resistance described here by Galileo is not that frequently accepted in the Middle Ages, which was held to arise either from light elements acting in an opposite direction to the predominant heavy elements of a body, or vice versa (see Selection 51.1 n. 9). Nor is it properly attributable to Duns Scotus or to Thomas Aquinas, as Galileo declares. Indeed, since no explicit statement is made by either Philoponus or Avempace (see n. 72), it is also highly questionable whether it is proper to interpret them as construing the weight (or force) of a body as a kind of resistance which is instrumental in producing finite motions in the void. There is, however, little doubt that such a position was distinguished in the Middle Ages (see Albert of Saxony’s discussion in Selection 47). It is worth noting that those who accepted the type of internal resistance arising from contrary tendencies of light and heavy elements would have rejected the assumption that a pure elemental body, say earth, could move with a finite speed in a hypothetical void. However, this assumption would probably have been adopted by those who accepted the internal resistance described by Galileo.—Ed.]

^72. Galileo’s meaning may be clarified by the memorandum (410.21–26): "Philoponus, Avempace, Avicenna, Saint Thomas, Scotus and others who try to maintain that motion takes place in time [i.e., not instantaneously] in the void, are mistaken when they assert a twofold resistance in the moving body, viz., one accidental and due to the medium, the other intrinsic and due to the body’s own weight. These two resistances are clearly one, for the medium, insofar as it is heavier, both offers more resistance and [by that very fact] renders the body lighter."

That is, though one may, by abstracting, analyze the weight of a body into two factors (weight of the body in a void, and weight of the medium in a void), these factors do not act independently and are not separable in the actual case of a body in a medium.

^73. "Decrease or increase" seems to be a slip for "increase or decrease."